Limits and Colimits
Category Theory II 1.2: Limits Category Theory II 2.1: Limits, Higher order functors Category Theory II 2.2: Limits, Naturality Category Theory II 3.1: Examples of Limits and Colimits
极限和余极限
在范畴论中,所有事物之间都是有联系的,我们可以从任意角度对它们进行考察。例如对积的泛构造,现在我们已经了解了函子和自然变换,那么这个泛构造是否可以简化甚至泛化?下面尝试一下
积的构造始于对两个对象a和b的选择,我们想要构造这二者的积。首先,“选择对象”到底意味着什么?我们能否用范畴论中的术语来描述这一动作?两个对象形成了一个非常简单的模式,我们可以将这个模式抽象到一个非常简单的范畴。我们将这个范畴称为2,它只包含了1和2两个对象,除了两个必须存在的恒等态射,也没有其他态射了。现在可以将“从范畴C中选择两个对象”的行为表述为“定义一个从范畴2到范畴C的函子D”。一个函子将对象映射到对象,因此它的象只是两个对象(也可能是一个,若该函子映射对象时有坍缩行为的话);函子也映射态射,在当前情况下只是将恒等态射映射成恒等态射。
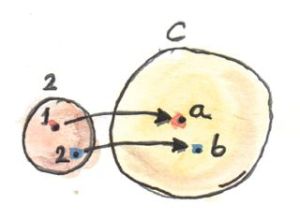
这种方式的优点它建立在范畴概念上,避免了“选择对象”这种不确切描述。此外,它也很容易概括,因为很容易就能用比2更复杂的范畴来定义模式。
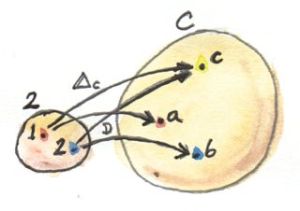
继续,定义一个积的下一步便是对候选对象c的选择。再次对“选择”换个说法,将之描述成从单例范畴出发的函子。(实际若是用Kan extensions来表述就好多了,但尚未接触这一概念,因此这里用了一点小技巧)从范畴2到范畴C的常量函子Δ。
Here again, we could rephrase the selection in terms of a functor from a singleton category. And indeed, if we were using Kan extensions, that would be the right thing to do. But since we are not ready for Kan extensions yet, there is another trick we can use: a constant functor Δ from the same category 2 to C. The selection of c in C can be done with Δc. Remember, Δc maps all objects into c and all morphisms into idc.