范畴 / Category

一些事物（称为对象/object）及事物之间的关系（称为态射/morphism）构成一个范畴。

最小的范畴是拥有0个对象的范畴。因为没有对象，自然也就没有态射。

可以通过用态射将对象连接起来的方法构造出范畴。

给出一个有向图，将它的结点视为对象，将节点间的箭头视为态射。在这个有向图上增加箭头，就可以将之构造成范畴。首先为每个结点添加恒等箭头，然后为所有首位相邻的箭头（即符合复合条件）增加复合箭头。注意每次新增一个箭头，必须考虑它本身与其它箭头（除了恒等箭头）的复合。这种由给定的图产生的范畴，称为自由范畴。以上是一种自由构造的示例，即给定一个结构，用符合法则（在此，就是范畴论法则）的最小数量的东西来扩展它。

编程语言中，一般是类型体现为对象，函数体现为态射。

复合 / Composition

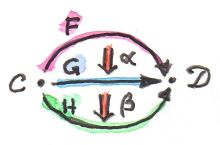
范畴的本质是复合，或者说复合的本质是范畴。若有从对象A到对象B的态射，也有从对象B到对象C的态射，那么必定存在从对象A到对象C的复合态射。

数学中，一般以 $g \circ f$ 表示函数复合（复合顺序从右向左，即 $g \circ f = \lambda x.g \lparen f \lparen x \rparen \rparen$，可读作“g after f”）。下以几种函数式编程语言进行复合思想的演示

1
2
3
4
5
6
7

-- Haskell

-- Haskell中，小写字母表示类型参数，具体类型是大写字母开头
f :: a -> b     -- 接受a返回b的函数
g :: b -> c     -- 接受b返回c的函数
-- 用`.`符进行复合，同数学写法一致，从右向左
g . f           -- f g 复合，其签名 `a -> c`

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// F#

// F# 中无 `Bottom Type` 的概念。F#中以`'`作为前缀的类型名称视为类型参数
let f : 'a -> 'b = fun x -> failwith "not implement"
// let f<'a, 'b> : 'a -> 'b = failwith "not implement" -- 另一种方式
let g : 'b -> 'c = fun x -> failwith "not implement"

// 用内置操作符`>>` `<<`进行复合，前者从左向右，后者从右向左
f >> g          // 从左向右复合
g << f          // 从右向左复合

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

// Scala

// Scala 中 `???` 是个 `Nothing` 类型值，`Nothing` 是Scala中的"Bottom Type"

// Scala中的方法/Method 函数/Function 函数值/Function Value 概念存在区别和联系
//   方法强调的是“实例方法”，是在“对象实例”上进行调用的。在trait、class中以`def`关键字定义的有参值是方法（Scala模糊了无参方法和属性的界限，无参方法可以不带括号调用求值）
//   函数无需任何实例即可调用，一般只能进行形如`func(arg)`的调用求值操作。在object、函数中以`def`关键字定义的可视为函数
//   函数值可视为一个函数实例，可以调用其实例方法。以λ给出的值、函数经`func _`转换的值、方法经`obj.method _`转换的值都是函数值，可将该值绑定到`funcVal`上
//      `funcVal.apply(arg)` 传入参数求值（可以直接这样用`funcVal(arg)`，会转换成对`apply`方法的调用）
//      `funcVal.compose(funcVal')` 传入另一个函数值，进行函数复合，其顺序从右向左
//      `funcVal.andThen(funcVal')` 传入另一个函数值，进行函数复合，其顺序从左向右
//      ...
//      注：`andThen` `compose`方法混入自`Function1`特质 (仅`Function1`特质定义了此方法，换言之，仅单参数列表、单参数函数才能进行复合)
//
// Scala中的函数和方法可以是参数多态/泛型的，但函数值必定是确定类型的

// Scala中函数不是自动柯里化/Currying，只能以定义多参数列表函数的形式进行显式柯里化（λ表达式写出柯里化不需任何特殊处理）
//      def func(x: A)(y: B)(z: C): X = ???
//      val func = (x: A) => (y: B) => (z: C) => ???
//      val func: A => B => C => X = x => y => z => ???

val f : A => B = ???
val g : B => C = ???
g compose f     // 从右向左复合，方法作为中缀操作符形式
g.compose(f)    // 从右向左复合，实例方法调用形式
f andThen g     // 从左向右复合，方法作为中缀操作符形式
f.andThen(g)    // 从左向右复合，实例方法调用形式

态射的复合需要满足以下两个性质

1. 结合律 / associative

   复合要满足结合律。若有三个态射 $f$ $g$ $h$ 可被复合（即对象可被首尾相连），必有 $h \circ \lparen g \circ f \rparen$ = $\lparen h \circ g \rparen \circ f$ = $h \circ g \circ f$。下面编程语言中以伪代码演示该性质（编程语言未定义“函数相等”）

   1 2 3 4 5

   -- Haskell f :: A -> B g :: B -> C h :: C -> D h . (g . f) == (h . g) . f == h . g . f

   1 2 3 4 5 6

   // F# let f : 'a -> 'b = fun x -> failwith "not implement" let g : 'b -> 'c = fun x -> failwith "not implement" let h : 'c -> 'd = fun x -> failwith "not implement" h << (g << f) == (h << g) << f == h << g << f // 从右向左复合 f >> (g >> h) == (f >> g) >> h == f >> g >> h // 从左向右复合

   1 2 3 4 5 6

   // Scala val f : A => B = ??? val g : B => C = ??? val h : C => D = ??? h compose g compose f // 从右向左复合 f andThen g andThen h // 从左向右复合

   对于函数复合的结合律，以上演示应当还是比较显而易见，但是在其它范畴中，可能结合律并不是那么显然。

2. 恒等态射 / identity morphism

   范畴中的任一对象，都存在恒等态射。这个态射从自身出发又返回自身。它是复合的最小单位。恒等态射与任何（符合复合条件的）态射复合，得到的都是后者自身。恒等态射称为$id_A$（意为 identity on A，即A与自身恒等）。

   在数学中，若有接受$A$返回$B$的函数$f$，则有$f \circ id_A = f$ 和 $id_B \circ f = f$

   编程语言中的实现很简单，只需要简单地把输入返回即可（一般函数式编程语言标准库中已有该基本元素）

   1 2 3 4 5 6 7 8

   -- Haskell id :: a -> a -- `id` 的函数签名，接受任意类型并返回此类型 id x = x -- `id` 的定义 注：Haskell标准库（称为Prelude）已定义 f :: a -> b -- 它与恒等函数复合之后还是其自身， 注：Haskell中是从右向左复合 id . f == f -- 这里的 `id` 是 `id_b` f . id == f -- 这里的 `id` 是 `id_a`

   1 2 3 4 5 6 7 8 9 10 11 12 13

   // F# // FSharp.Core 中 `id` 的定义、并以特性方式注明了编译成程序集之后的名称 [<CompiledName("Identity")>] let id x = x // F#具备自动泛化/Automatic Generalization特性，其类型是 `id : 'a -> 'a` let f : 'a -> 'b = fun x -> failwith "not implement" id >> f == f // 从左向右复合，此处 `id` 是 `id_a` f >> id == f // 从左向右复合，此处 `id` 是 `id_b` id << f == f // 从右向左复合，此处 `id` 是 `id_b` f << id == f // 从右向左复合，此处 `id` 是 `id_a`

   1 2 3 4 5 6 7 8 9 10 11 12

   // Scala // scala-library 中 `identity` 的定义，标注了 `@inline` @inline def identity[A](x: A): A = x val f : a => b = ??? (identity[b] _) compose f == f // 从右向左复合，此处 `identity` 是 `identity_b` f compose identity[a] == f // 从右向左复合，此处 `identity` 是 `identity_a` f andThen identity[b] == f // 从左向右复合，此处 `identity` 是 `identity_b` (identity[a] _) andThen f == f // 从左向右复合，此处 `identity` 是 `identity_a`

函数 / Function

数学上的函数是值到值的映射。在编程语言中，可以实现数学上的函数：一个函数，给它一个输入值，它就计算出一个结果。每次调用时，对于相同输入，总能得到相同的输出。

编程语言中，给出相同输入保证得到相同输出，且对外界环境无关的函数，称为纯函数。纯函数式语言Haskell中，所有函数都是纯的。对其它语言，可以构造一个纯的子集，谨慎对待副作用。之后将会看到单子如何只借助纯函数对副作用进行建模。

Set

Set是集合的范畴。在Set中，对象是集合，态射是函数。

存在一个空集 $\emptyset$，它不包含任何元素；也存在只有一个元素的集合。函数可以将一个集合中的元素映射到另一个集合；也能将两个元素映射为一个。但是函数不能将一个元素映射成两个。恒等函数可以将一个元素映射为本身。

类型 / Type

范畴中，并非任意两个态射皆可复合。当某态射的源与另一态射的目标是同一对象时，两态射才能复合。在编程语言中，类型关乎复合。在参数及返回类型上，两函数必须满足复合条件，这样在类型意义上程序才是安全的（当然，这一般仅是程序通过编译的保证，并非逻辑正确的保证）。

对于类型，一个直观理解是：类型是值的集合。例如，Bool类型是2个元素True False的集合，Char类型是所有Unicode字符的集合。集合可能是有限的（例如Bool），也可能是无限的（例如String）。当声明x :: Integer时，是在说x是整型数集中的一个元素。

理想世界中，可以说Haskell的数据类型是集合，Haskell的函数是集合之间的数学函数。但由于“数学函数只知道答案，不可被执行”，Haskell必须要计算才能得出答案。若是可以在有限步骤内计算完毕，这没有什么问题，但有些计算是递归的，可能永远不会终止。在Haskell中无法阻止无终止的计算（停机问题）。Haskell为每个类型添加了一个特殊值，称为底/Bottom，用符号表示为_|_或⊥。这个值与无休止计算有关。若一个函数声明为f :: a -> Bool，它可以返回True False或_|_，后者表示它不会终止。

将底作为类型系统的一部分之后，可以将运行时错误作为底对待，甚至可以允许函数显式地返回底（一般用于未定义表达式）。例如声明f :: a -> Bool 定义f x = undefined。因为undefined求值结果是底，它可以是任何类型的值，因此该定义可以通过类型检查。（甚至f = undefined，因为底也是a -> Bool这种类型的值）。

可以返回底的函数称为偏函数；全函数则可以保证对任意参数返回有效的结果。

由于底的存在，Haskell的类型与函数的范畴称为Hask而不是Set。从实用的角度看，可以暂时无视掉这些无终止的函数与底，将Hask视为一个友善的Set即可。

注：Scala中也有底类型的概念存在，Nothing是任何类型/Any的子类型，Null是所有引用类型/AnyRef的子类型。F#中没有这一概念。

基于类型是集合的直觉，思考一些特殊情形。

• 空集

  在Haskell中，空集是Void，这是个没有任何值的类型。可以定义一个接受Void的函数，但是无法调用它。因为无法提供一个Void类型的值（这种值不存在）。该函数的返回值没有任何限制，这是个多态返回类型的函数。Haskell中该函数称为absurd :: Void -> a。这种类型与函数，在逻辑学上有更深入的解释。Void表示谎言，absurd函数的类型相当于“由谎言可以推出任何结论”，这也就是逻辑学中的“爆炸原理”。

  F# 和 Scala 中似乎没有 空集/Void 的概念 ？

• 单例集合

  这是只有一个值的类型。它实际上是其它编程语言如C++/Java中常见的void类型。考虑一个函数int f42() {return 42;}。已知无法调用不接受任何值的函数，函数f42被调用时发生了什么？从概念上说，接受了一个空值。由于不会有第二个空值，所以没有显式强调它。在Haskell中为空值提供了一个符号()（读作"unit"，该符号既是类型也是值）

  F#中，空值的类型为unit，值为()；Scala中空值类型为Unit，值为()，它是AnyVal的子类型。

  注意，每个接受unit的函数都等同于从目标类型中选择一个值的函数。实际上，可以将f42作为数字42的另一种表示方法，这也演示了如何通过与函数交互来代替显式给出集合中某个元素。这证实了数据与计算过程在本质上是没有区别的。从unit到类型A的函数就相当于集合A中的元素。

  考虑让函数返回一个unit的情形。在C++等其它编程语言中，这样的函数通常担当含有副作用的函数，这并非数学意义上的函数。一个返回unit类型的纯函数，它什么也不做；或者说，唯一做的就是丢弃接受的输入。

  1 2 3

  -- Haskell 中的 `unit` 函数 unit :: a -> () unit _ = ()

  1 2 3 4

  // F# 中的 `ignore` 函数 // ignore : 'a -> unit [<CompiledName("Ignore")>] let inline ignore _ = ()

  Scala中好像没有类似的函数

• 二元集合

  二元集合一般对应编程语言中的布尔类型。命令式/面向对象编程语言中，该类型一般是内置的bool。但在Haskell中可以自行定义 data Bool = True | False（读作Bool要么是True要么是False）。（F#中也可以直接进行定义type Bool = True | False，Scala中需要借助封闭抽象类/sealed abstract class来定义）

  接受Bool的纯函数只是从目标类型中选择了两个值，一个关联了True，另一个关联了False。返回Bool的函数被称为“谓词/predicate”。

  注： 二元集合并非只有Bool，自定义类型也可能是个二元集合（例如type Gender = Male | Female）

Hom-集 / Hom-Set

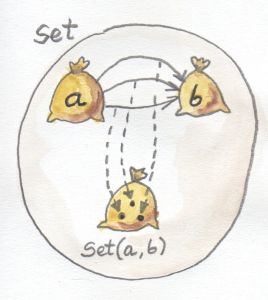
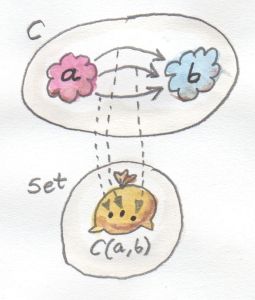
在一个范畴C中，从对象a到对象b的态射集称为hom-集，记作C(a,b)或$Hom_C\lparen a,b \rparen$。

在集合范畴中，hom-集自身也是个对象，因为它也是个集合，这种称为内hom-集，如左图所示；对于其它范畴，hom-集只是个范畴之外的集合，这种被称为外-hom集，如右图所示

序 / Order

存在这样的范畴，其中态射描述两个对象之间的小于等于关系（这是个范畴。每个对象都小于等于自身，因此恒等态射存在；若$a \le b$且$b \le c$，则$a \le c$，态射复合存在；另，态射复合遵守结合律）。伴随这种关系的集合称为前序集/preorder，一个前序集是一个范畴。

可以加强这种对象间的关系，要求该关系满足一个附加条件，即，若$a \le b$且$b \le a$，则必有$a = b$。伴随这种关系的集合称为偏序集/partial order。

若一个集合中的任意两个元素之间存在偏序关系，这种集合称为全序集/total order。

可将这些有序集描绘为范畴。前序集所构成的范畴，在任意两个对象之间最多只有一个态射，这样的范畴称为瘦范畴。瘦范畴内的每个hom-集要么是空集，要么是单例/singleton。在任意前序集构成的范畴内，C(a,a)也是个单例hom-集，只包含恒等态射。前序集中是允许出现环的，但偏序集中不允许。

排序需要用到前序、偏序和全序的概念。例如快排、归并之类的排序算法，只能在全序集中进行；偏序集可以用拓扑排序来进行处理。

幺半群 / Monoid

幺半群是个简单且重要的概念，它是基本算术幕后的概念：只要有加法或乘法运算就可以形成幺半群。编程中幺半群有很多实例，表现为字符串、列表、可折叠数据结构、并发编程中的future、函数式响应编程中的事件等。

数学上，幺半群$\langle S, *, e \rangle$是指一个带有可结合二元运算($*: S \times S \rightarrow S$，这隐含了$S$对运算$*$封闭)和单位元$e$的代数结构$S$。“可结合”是指二元运算满足结合律，$\forall a,b,c \in S \Rightarrow \lparen a * b \rparen * c = a * \lparen b * c \rparen$；单位元是指，$\exists e \in S \And \forall a \in S \Rightarrow a * e = e * a$

Set伴随笛卡尔积运算便构成幺半群，其幺元是单例；Set伴随“不交并/Disjoint Union”运算也构成幺半群，其幺元是空集。

个人理解：Cat中，对象是范畴，态射是函子。其构成幺半群所需的二元运算即为“二元函子”。

• 作为集合

  伴随着一个满足结合律的二元运算和一个特殊“中立”元素的的集合被称为幺半群。对与该二元运算，这个“中立”元素的行为类似一个返回其自身的“unit”。

  例如，加法运算和包含0的自然数集便形成一个幺半群。结合律是指(a+b)+c=a+(b+c)或$\lparen a + b \rparen + c = a + \lparen b + c \rparen$。这个理想的、永远保持“中立”的元素是0，因为0+a=a以及a+0=a（$0+a=a$ $a+0=a$）。由于加法满足交换律（a+b=b+a $a+b=b+a$），所以似乎再强调a+0=a有点多余。但应注意，交换律并非幺半群所需。例如，字符串连接运算不遵守交换律，但字符串及其连接运算可以构成幺半群，它的中立元素是空字符串。

• 作为范畴

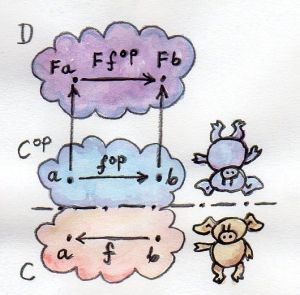
  幺半群可被描述为带有一个态射集的单对象范畴，这些态射皆符合复合规则。

  只含单个对象m的范畴M存在hom-集M(m,m)。在这个集合上可以定义一个二元运算，M(m,m)中两元素“相乘”相当于两态射的复合。复合总是存在的，因为这些态射的源对象与目标对象是同一个对象。这种“乘法运算”也符合范畴论法则中的结合律，因为态射复合满足结合律。恒等态射也是肯定存在的。因此，总是能够从幺半群范畴中复原出幺半群集合。因此，幺半群范畴与幺半群集合是同一个东西。

  在范畴论中，是在尝试放弃查看集合及其元素，转而讨论对象和态射。因此，现从范畴的角度来看作用于集合的二元运算。

  例如，一个将每个自然数都加5的运算（会将0映射为5、将1映射为6等等）这样就在自然数集上定义了一个函数，现在有了一个函数与一个集合。通常对于任意数字n，都会有一个加n的函数，称之为“adder”。把这些“adder”采用符合直觉的方式去复合，例如adder5与adder7的复合式adder12。因此“adder”的复合等同于加法规则，现在可以用函数的复合来代替加法运算。此外，还有一个面向中立元素0的adder0，它不会改变任何东西，因此它是自然数集上的恒等函数。

  每个范畴化的幺半群都会定义一个唯一的伴随二元运算的集合的幺半群，事实上总是能够从单个对象的范畴中抽出一个集合，这个集合是态射的集合。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

-- Haskell

-- 定义 `Monoid` 类型类
class Monoid m where
    empty :: m
    append :: m -> m -> m   -- currying form

-- 将 `String` 声明为一个 `Monoid` ，提供 `empty` `append` 的实现
instance Monoid String where
    empty = ""
    append = (++)      -- 中缀运算符用括号包住后，就转化为接受两个参数的函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

// F#

// F# 中不存在 类型类/type class 的概念，参考Scala版本尝试给出了使用接口进行的定义
module Monoid =
    open System         // `String`类存在于`System`名称空间下，或者可以直接用F#为之给出的类型别名：`string`，此处是为了形式一致
    type Monoid<'T> =   // F# 中定义泛型类型时，写法可以是`type 'T Monoid`或`type Monoid<'T>`
        abstract member Zero: 'T
        abstract member BiOp: ('T -> 'T -> 'T)      // 注意，此处给出`BiOp`的类型`('T -> 'T -> 'T)`时带上了括号

    let stringMonoid = {    // 使用对象表达式，直接实例化一个实现了接口的匿名类对象。
        new Monoid<String> with
            member _.Zero = ""
            member _.BiOp = (+)
        }

    type StringMonoid =     // 似乎基于对接口的实现来定义一个新的类并不合适，似乎不太符合"Monoid"的意义
        interface Monoid<String> with    // 也可以写作`String Monoid`
            member _.Zero = ""
            member _.BiOp = (+)

    // ---------------------------

    // F#是一门混合范式语言，一般是函数式编程范式优先。涉及到与面向对象范式混合编程时，存在一些注意事项
    // 在函数式世界里，函数是一等公民，可以作为值来用。
    //      `fun x -> x + 1` 是一个匿名函数值，与数字`1` 字符串`"abc"`的身份没有高低之分
    //      `let add1 = fun x -> x + 1` 是在将“函数值”绑定到名称`add1`上，与`let a = 1`在做的事情没有区别
    //      `let add' = add1` 是在将`add1`的值绑定到名称`add'`上，与`let b = a`行为类似
    // 面向对象的世界里函数/方法并非一等公民，是有特殊处理的
    type I<'T, 'R> =                    // 定义一个泛型接口
        abstract member M1: 'T -> 'R    // 没有括号，这是在定义接受`'T`返回`'R`的函数
        abstract member M2: ('T -> 'R)  // 带上括号，这是在定义`FSharpFunc<'T,'R>`(`'T -> 'R`)类型的只读属性
    type C<'T, 'R>() =                  // 定义一个泛型类型
        let f:'T->'R = failwith "err"   // 私有的函数类型字段
        interface I<'T, 'R> with        // 该类实现泛型接口
            member _.M1 t = f t         // 实现接口中定义的方法，必须显式给出参数。调用时使用`obj.M1(x)`方式
            member _.M2 = f             // 实现接口中定义的属性，只能直接赋函数值。这是`FSharpFunc<'T,'R>`类型的属性，注意与`Func<T,R>`类型不同

    // ---------------------------

    // 使用Monoid实例的时候，似乎可以考虑使用静态解析类型参数来进行约束，而不必要求必须是某个接口的实现 ??
    // 尝试实现失败
    // Constraints: https://docs.microsoft.com/en-us/dotnet/fsharp/language-reference/generics/constraints
    // Statically Resolved Type Parameters: https://docs.microsoft.com/en-us/dotnet/fsharp/language-reference/generics/statically-resolved-type-parameters
    // Type extensions: https://docs.microsoft.com/en-us/dotnet/fsharp/language-reference/type-extensions
    // 静态解析的类型参数: https://docs.microsoft.com/zh-cn/dotnet/fsharp/language-reference/generics/statically-resolved-type-parameters
    // 只有在定义时或内部类型扩展(Intrinsic type extensions)给出的成员才是符合静态类型约束的
    // 类型扩展: https://docs.microsoft.com/zh-cn/dotnet/fsharp/language-reference/type-extensions#optional-type-extensions

    // todo: 等到F#5发布，扩展成员可以作为满足约束的证据
    // 参考ISSUE：[RFC FS-1043] Extension members visible to trait constraints #6805： https://github.com/dotnet/fsharp/pull/6805
    // RFC： https://github.com/fsharp/fslang-design/blob/master/RFCs/FS-1043-extension-members-for-operators-and-srtp-constraints.md

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

object Monoid {
    trait Monoid[M] {
        def zero : M
        def biOp : (M, M) => M
    }

    val stringMonoid = new Monoid[String] {
        def zero = ""
        def biOp = _ + _
    }

    class StringMonoid extends Monoid[String] {
        def zero = ""
        def biOp = _ + _
    }
}

// -------------------------
trait T[A, B] {         // 定义一个泛型特质，该特质将会被编译成java interface
    val value: A        // 在特质中定义一个A类型的值，将会被编译成接口中一个返回A的无参方法
    def p: A => B       // 在特质中定义一个`A=>B`类型的值，将被编译成一个返回`A=>B`/`Function1[A,B]`的无参方法
    def m(a: A): B      // 在特质中定义一个接受A返回B的方法，将被编译成一个普通的接口方法
}

注：概念上 append = (+) 与 append s1 s2 = (+) s1 s2 是不同的。前者是Hask范畴（忽略"Bottom Type"的话则是Set）中态射的相等，这样不仅写法简洁，也经常被泛化到其它范畴。后者称为外延相等/extensional equality，陈述的是对任意两个输入，append 与 (+) 的值是相同的。由于参数的值有时也被称为point（函数$f$在点$x$出的值），外延相等也被称为point-wise相等，未指定参数的函数相等称为point-free相等。

同构 / Isomorphism

数学上，意味着存在一个从对象a到对象b的映射，同时也存在一个东对象b到对象a的映射，这两个映射是互逆的。在范畴论中，用态射取代映射。一个同构是一个可逆的态射；或者是一对互逆的态射。

可以通过复合与恒等来理解互逆：若态射g与态射f的复合结果是恒等态射，那么g是f的逆。这体现为以下两个方程(因为两个态射存在两种复合形式) f . g = id g . f = id

初始对象 / Initial Object

推广对象的“序”的概念，若存在一个从对象a到对象b的态射，那么认为对象a比对象b更靠前。在范畴中，若存在一个对象，它发出的态射指向所有其它对象，那么这个对象就是初始对象。对于给定范畴，可能无法保证初始对象的存在；也可能存在很多个初始对象。考虑有序范畴，在有序范畴中，任意两个对象之间，最多只允许存在一个态射。基于此，给出初始对象定义

初始对象：有且仅有一个态射指向范畴中任意一个对象。

以上定义主要是为了让初始对象在同构意义下具备唯一性。(意思是任意两个初始对象都是同构的。)

假设两个初始对象$i_1$ $i_2$。由于$i_1$是初始对象，因此有唯一的态射f从$i_1$到$i_2$；同理也有唯一的态射从$i_2$到$i_1$。考虑这这两个态射的复合，$g \circ f$必定是$i_1$到$i_1$的态射，由于$i_1$是初始对象，只允许一个$i_1$到$i_1$态射的存在。在范畴中，$i_1$到$i_1$态射是恒等态射，因此$g \circ f$等同于恒等态射。同理，$f \circ g$也是恒等态射。这样就证明了f与g互逆，因此两个初始对象是同构的。

例如，偏序集的初始对象是那个最小的对象。但是，有些偏序集（如整数集）没有初始对象。集合范畴中，初始对象是空集。Haskell中空集对应物是Void类型，从Void到任意类型的多态函数是唯一的，称为absurd :: Void -> a，这是一个态射族，由于该态射存在，Void才称为类型范畴中的初始对象。

终端对象 / Terminal Object

终端对象：有且仅有一个态射来自范畴中的任意对象。同样，终端对象在同构意义下具备唯一性。

偏序集内，若存在终端对象，那么它是最大的那个对象。集合范畴中，终端对象是个单例，即()，有且仅有一个纯函数，从任意类型到unit类型unit :: a -> () （注意，唯一性的条件十分重要。因为有些集合，实际是除了空集的所有集合会有来自其它集合的态射，例如存在函数yes :: a -> Bool yes _ = True，但是Bool并不是终端对象，因为还有 no :: a -> Bool no _ = False。）

对偶 / Duality

对于任意范畴C，反转态射方向、重新定义态射复合方式即可定义一个相反的范畴C’。这个对偶范畴自然能满足所有的范畴性质。原始态射f :: a -> b g :: b -> c用h = g . f复合得到h :: a -> c，那么在对偶范畴中 f' :: b -> a g' :: c -> b用h' = f' . g'复合得到h' :: c -> a。恒等态射保持不变。

一个范畴中的初始对象，在另一个范畴中就是终端对象。

泛构造 / Universal Construction

范畴论中一个常见的构造，称为泛构造，是通过对象之间的关系来定义对象。

给出一个模式(由对象与态射构成的一种特殊的形状)，然后在范畴中观察它的各个方面。如果这个模式很常见且范畴也很大，将会有大量的符合这个模式的东西。然后对这些符合模式的东西进行排序，并选出最好的那个。一般来说，给出排序规则的时候需要一定技巧。

下以积/Product和余积/Coproduct对泛构造的思想进行演示。

积 / Product

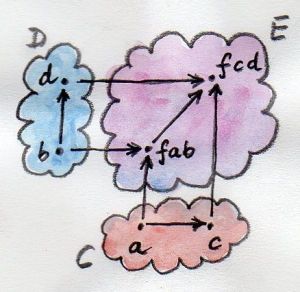
已知两个集合的笛卡尔积的概念，这个笛卡尔积是个元组/序对的集合。基于此，尝试提取出“积集合”与“成分集合”之间存在的连接模式，这个连接模式便可推广到其它范畴。

积存在两个投影p和q可将积投影成单个成分。借助此，尝试定义集合范畴中对象和态射的模式，这种模式可以引导构造两个集合a与b的积。这个模式由对象c和两个态射p::c->a及q::c->b构成。所有的符合这种模式的c都可以看作一个候选积，这样的c会有很多。

第二步涉及到泛构造的另一方面：排序，或者说对比。需要有这么一个规则，能取对比符合给出模式的两个实例，最终找出最好的那个。现有两个候选，c和p::c->a及q::c->b、c'和p'::c'->a及q'::c'->b，若存在一个态射m::c'->c，且由此m能重新构造p'=p.m和q'=q.m，由此可确定c比c'“更好”。另一个看待这些等式的视角是：m看作一个因子，它能将p'和q'进行“因式分解”。下图给出更直观的复合关系

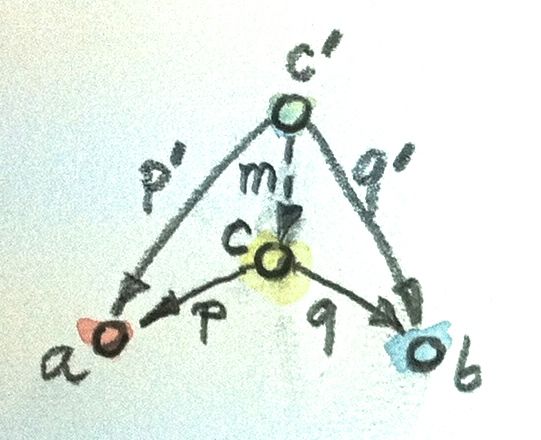
投影p和q在Haskell/F#中对应物为fst和snd，其作用是解构二元组。前者取第一个成分、后者取第二个成分。

例如，从类型中选择Int和Bool，取它们的积。将Int和(Int, Int, Bool)作为它们的候选积。一个Int就可作为Int与Bool的积，因为它具有p x = x和q _ = True，这样它就符合了候选积的条件；单个Bool同理。三元组(Int, Int, Bool)也是一个合理的候选积，因为具备p (x, _, _) = x和q (_, _, b) = b。能够注意到，第一个候选积太小了，它只覆盖了Int方面，第二个候选积又太大了，包含了一个无用的Int维。

现在演示(Int, Bool)二元组及其映射fst和snd为何比前面给出的候选积更好。参考下图，对于Int，存在一个m::Int->(Int,Bool)例m x = (x,True)，那么伴随Int的p q可以这样构造p x = fst (m x) = x及q x = snd (m x) = True；同理，伴随三元组的m可以这样实现m (x,_,b) = (x,b)。

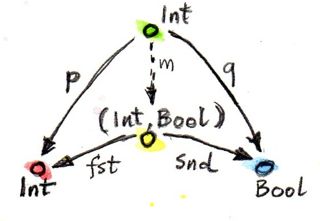
已经证明了(Int, Bool)为何优于另外两者，但仅这样似乎不够完全说服人，因此此处再给出为何反过来就不成立。对于Int，是否能找到一个m'用于从p q构造出fst snd？假如存在，那么就有fst = p . m' snd = q . m'，已知伴随Int的q永远是True，而(Int, Bool)元组中第二成分是False的二元组确实存在，因此永远无法从q构造出snd。而对于(Int, Int, Bool)情况就不一样了，总是可以得到足够的信息，但是这里却存在无数个m'可以去对fst snd进行“因式分解”，例如m' (x, b) = (x, x, b) m' (x, b) = (x, 42, b)等无数个实现。

综上，给出任意类型c和两个投影p及q，有唯一的从c到笛卡尔积(a,b)的“因子”m，可以对p q进行“因式分解”。事实上，这个m只是把p和q的结果放到了元组 m::c->(a,b)、m x = (p x, q x)。这使得笛卡尔积(a,b)成为了“最好”的符合“积模式”的候选。此外，这也意味着泛构造在集合范畴上运行效果良好，它也指出了任意两个集合的积是什么。

现在，使用相同的泛构造来定义任意范畴中两对象的积。这个积不保证一定存在，但若存在，它就在同构意义下是唯一的，且这个同构是唯一的。

A product of two objects a and b is the object c equipped with two projections such that for any other object c’ equipped with two projections there is a unique morphism m from c’ to c that factorizes those projections.

对象a和b的积是伴随这两个投影的对象c，对任意其它伴随两个投影的对象c'，存在唯一的态射m :: c' -> c，可以用这个m对c'的两个投影进行“因式分解”。

因子生成器/factorizer是能生成因子m的高阶函数。factorizer :: (c -> a) -> (c -> b) -> (c -> (a, b)) 其实现 factorizer p q = \x -> (p x, q x)

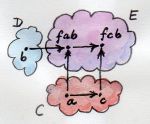
余积 / Coproduct

同范畴论中每个构造一样，积的对偶是余积。将积范式中态射的方向反转，便得到了一个对象c伴随着两个入射i :: a -> c和j :: b -> c。对符合余积模式构造的排序方式也反转了，若存在一个态射m :: c -> c'，能对伴随c'的入射i' :: a -> c'及j' :: b -> c'进行“类因式分解”，即i' = m . i及j' = m . j，如下图所示。因此这个“最好”的对象，对任意的其它模式都有一个唯一的态射“发射”出去，这个对象就是余积。只要它存在，那么它在同构意义上就是唯一的，且这个同构也是唯一的。

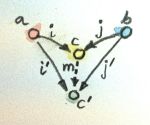
A coproduct of two objects a and b is the object c equipped with two injections such that for any other object c’ equipped with two injections there is a unique morphism m from c to c’ that factorizes those injections.

对象a与b的余积是对象c伴随着两个入射i::a->c及j::b->c，对于其它任意的对象c'及伴随其的入射i'::a->c'及j'::b->c'，存在唯一的态射m::c->c'，且该态射可以作为“因子”分解i'及j'

在集合范畴中，余积就是两个集合的不相交求并运算。集合 a 与集合 b 的不相交求并结果中的一个元素，要么是 a 中的元素，要么是 b 中的元素。若两个集合有交集，那么余积会包含公共部分的两份拷贝。可将不相交求并运算结果的一个元素想象为贴着它所属集合的标签的元素。

也可以为余积定义一个因式生成器。对于给定的候选余积 c 以及两个候选入射 i 与 j，为 Either生成因式函数的的因式生成器可定义为：

1
2
3

factorizer :: (a -> c) -> (b -> c) -> Either a b -> c
factorizer i j (Left a)  = i a
factorizer i j (Right b) = j b

非对称 / Asymmetry

目前已知两种对偶结构，终端对象可由初始对象经箭头反转后获得，余积可由积经箭头反转而获得。但在集合范畴中，初始对象与终端对象的行为有显著区别，积与余积也有显著区别。积的行为像是乘法运算，终端对象扮演者 1 的角色；余积的行为更像求和运算，初始对象扮演着 0 的角色。特定情况下，对有限集，积的尺寸就是各个集合的尺寸的积；余积的尺寸是各个集合的尺寸之和。

这一切都表明了集合的范畴不会随箭头的反转而出现对称性。

注：空集可以向任意集合发出唯一态射（absurd函数），但它没有其他集合发来的态射。单例集合拥有任意集合发来的唯一的态射，但它也能向任意集合（除了空集）发出态射。由终端对象发出的态射在拮取其他集合中的元素方面扮演了重要的角色（空集没有元素，因此没什么东西可拮取）

下面理解一下单例()作为积和作为余积。

将单例()配备两个投影p与q将之作为候选积。由于积是泛构造，存在态射m :: () -> (a, b)，这个态射从积集合中选出一个元素（即一个元组），它也可“因式化”两个投影：p = fst . m及q = snd . m。这两个投影作用于单例值()，上面那两个方程就变为：p () = fst (m ())及q () = snd (m ())。 由于m ()是m从积集合中拮取的元素(即一个元组)，p所拮取的是参与积运算的第一个集合中的元素，结果是p ()，同理q拮取的是参与积运算的第二个集合中的元素q ()。这完全符合对积的理解，即参与积运算的集合中的元素形成积集合中的序对/元组。

单例作为候选的余积，就不会它作为候选的积那样简单了。确实可以通过投影从单例中抽取元素，但是向单例入射就没有意义了，因为“源”在入射时会丢失。从真正的余积到作为候选余积的单例的态射也不是唯一的。集合的范畴，从初始对象的方向去看，与从终端对象的方向去看，是有显著差异的。

这其实不是集合的性质，而是是我们在 Set 中作为态射使用的函数的性质。函数通常是非对称的，下面我来解释一下。

函数是建立在它的定义域（Domain）上的（在编程中，称之为全函数），它不必覆盖余定义域（Codomain、陪域）。目前已经看了一些极端的例子（实际上，所有定义域是空集的函数都是极端的）：定义域是单例的函数，意味着它只在余定义域上选择了一个元素。若定义域的尺度远小于余域的尺度，通常认为这样的函数是将定义域嵌入余定义域中了。例如可以认为，定义域是单例的函数，它将单例嵌入到了余定义域中。将这样的函数称为嵌入函数，但是数学家给从相反的角度进行命名：覆盖了余定义域的函数称为满射（Surjective）函数或映成（Onto）函数。

函数的非对称性也表现为，函数可以将定义域中的许多元素映射为余定义域上的一个元素，也就是说函数坍缩了。一个极端的例子是函数使整个集合坍缩为一个单例，unit函数就是这种行为。这种坍缩只能通过函数的复合进行混成。两个坍缩函数的复合，其坍缩能力要强过二者单兵作战。数学家为非坍缩函数取了个名字：内射（Injective）或一对一（One-to-one）映射。

有许多函数即不是嵌入的，也不是坍缩的。它们被称为双射（Bijection）函数，它们是完全对称的，因为它们是可逆的。在集合范畴中，同构就是双射的。

代数数据类型 / Algebraic Data Type

编程中的积类型

两个类型的积，一般实现为序对(Pair)/元组。

序对并非严格可交换的：不能用(Int, Bool)直接替换(Bool, Int)，即便两者承载了同样的信息。在同构意义上序对是可交换的，swap :: (a, b) -> (b, a) swap (x, y) = (y, x)给出了同构关系，可以看作是不同的格式存储了相同的数据。

可通过序对的嵌套完成对任意个类型组合成积，运用“嵌套的序对与元组同构”这一事实可以使构造过程更简单。例如，序对嵌套可以是(a,(b,c))或((a,b),c)，两者并不相同，但所包含的元素是一一对应的，因此这是一种同构，用不同的方式包装了相同的数据。

可以将积类型的构造解释为作用于类型的一种二元运算。从这个角度来看，上述的同构关系看上去有些像幺半群中的结合律：(a * b) * c = a * (b * c)。只不过，在幺半群的情况中，这两种复合为积的方法是等价的，而上述积类型的构造方法只是在“同构条件下”等价。

如果在同构条件下，不再坚持严格相等的话，能揭示unit类型()类似于数字乘法中的 1。类型 a的值与一个unit值所构成的序对，除了a值之外再无其它。因此，这种类型(a, ())与a是同构的。

用形式化语言描述这些现象，可以说Set（集合的范畴）是一个幺半群范畴，亦即这种范畴也是一个幺半群，这意味着可以让两对象相乘（在此，就是两集合去构造笛卡尔积）。

Haskell中有一种更通用的办法来定义积类型 date Pair a b = P a b 在此，Pair a b是由a与b参数化的类型的名字；P是数据构造子的名字。要定义一个序对类型，只需向Pair类型构造子传递两个类型。要构造一个序对类型的值，只需向数据构造子P传递两个合适类型的值。类型构造子与数据构造子的命名空间是彼此独立的，二者可以同名：data Pair a b = Pair a b。可以发现，Haskell内置的序对类型只是这种声明的一种变体，前者将数据构造子 Pair 替换为一个二元运算符 (,)。将这个二元运算符像正常的数据构造子那样用，照样能创建序对类型的值。

如果不用泛型序对或元组，也可以定义特定的有名字的积类型，例如data Stmt = Stmt String Bool，它是 String 与 Bool 的积，有自己的名字与构造子。这种风格的类型声明，其优势在于可以为相同的内容定义不同的类型，使之在名称上具备不同的意义与功能，以避免彼此混淆。

F#中，可以type Pair<'a, 'b> = Pair of 'a * 'b来定义序对，其本质是定义了一个单例的union。

记录 / Record

记录是支持数据成员命名的积类型。

例如用两个字符串表示化学元素的名称与符号，用一个整型数表示原子量，将这些信息组合到一个数据结构中。可以用元组 (String, String, Int) 来表示这个数据结构，只不过需要记住每个数据成员的含义。这样的代码很容易出错，并且也难于理解与维护。更好的办法是用记录：data Element = Element { name :: String, symbol :: String, atomicNumber :: Int }，上述的元组与记录是同构的。

F#中，记录是这种语法type Element = {name:string; symbol:string, atomicNumber:int}

感觉也可以这样理解，在面向对象世界里，多个字段构成一个类，就是在构造一个积的过程。

类型可以看作集合，可以带上一些业务限制。例如班级信息包含年级、班、学生数量字段，这三者可以都是Int，但在业务意义上存在限制(例如1-6年级最多3个班最多60人)，可以看作(1~6) * (1~3) * (1~60)的积

编程中的和类型

余积在编程中的对应物是和类型。

Haskell官方实现的和类型是data Either a b = Left a | Right b。Either在同构的意义下是可交换的，也是可嵌套的，而且在同构意义下，嵌套的顺序不重要。因此可以定义出多个类型的和data OneOfThree a b c = Sinistral a | Medial b | Dextral c

Set对于余积而言也是个（对称的）幺半群范畴。二元运算由不相交和（Disjoint Sum）来承担，unit元素便是初始对象。用类型术语来说，可以将Either作为幺半群运算符，将Void作为中立元素。也就是说，可以认为Either类似于运算符+，而Void类似于0。这与事实是相符的，将 Void 加到和类型上，不会对和类型有任何影响。例如：Either a Void与a同构。这是因为无法为这种类型构造Right版本的值(不存在类型为Void的值)。Either a Void只能通过Left构造子产生值，这个值只是简单的封装了一个类型为a的值。这就类似于a + 0 = a。

Haskell中，可以将Bool实现为data Bool = True | False，就是两个单值的和。Maybe a = Nothing | Just a用于表示可能不存在，Nothing是个单值表示不存在，因此此定义可以理解成a+1，也可重定义成Maybe a = Either () a，用()表示不存在。data List a = Nil | Cons a (List a)，这是一个递归的和类型

F#中似乎没有Either的定义，若是用的到，可以自行定义type Either<'a, 'b> = Left of 'a | Right of 'b。存在type Option<'a> = None | Some of 'a或type ValueOption<'a> = ValueNone | ValueSome of 'a。List实现类似type List<'a> = [] | :: ('a * 'a list)

类型代数 / Algebra of Types

当前已有了类型系统中两种幺半群结构：以Void作为幺元的和类型、以()作为幺元的积类型。

将这两种构造想象为加法和乘法，在这个视角中，Void类似于0，()类似于1。这种视角是否符合一些事实，例如：与0相乘的结果依然是0，尝试构造一个(Int, Void)序对必定失败，因为不存在一个Void值，因此(Int, Void)等价于Void，即a * 0 = 0；数学加法和乘法存在分配律a * (b + c) = a * b + a * c，对于积类型与和类型而言，在同构意义上也存在分配律，例如：(a, Either b c) = Either (a, b) (a, c)

这种互相纠缠的幺半群称为半环/Semiring(之所以不是全环，是因为无法定义减法)。在此仅关心如何描述自然数运算与类型运算之间的对应关系。下表给出一些对应关系

列表类型List a = Nil | Cons a (List a)被定义为一个方程的解，因为要定义的类型出现在方程两侧，若将 List a 换成x，就可以得到这样的方程：x = 1 + a * x。

不过，不能使用传统的代数方法去求解这个方程，因为对于类型没有相应的减法与除法运算。不过，可以用一系列的替换，即不断的用 (1 + a*x) 来替换方程右侧的 x，并使用分配律，这样就有了下面的结果：

1
2
3
4
5

x = 1 + a*x
x = 1 + a*(1 + a*x) = 1 + a + a*a*x
x = 1 + a + a*a*(1 + a*x) = 1 + a + a*a + a*a*a*x
...
x = 1 + a + a*a + a*a*a + a*a*a*a...

最终会是一个积（元组）的无限和，这个结果可被解释为：一个列表，要么是空的，即 1；要么是一个单例 a；要么是一个序对 a*a；要么是一个三元组 a*a*a；……以此类推，结果就是一个由 a 构成的串。

用符号变量来解方程，这就是代数！因此上面出现的这些数据类型被称为：代数数据类型。

注：类型a与类型b的积必须包含类型a的值与类型b的值，这意味着这两种类型都是有值的；两种类型的和则要么包含类型a的值，要么包含类型b的值，因此只要二者有一个有值即可。逻辑运算and与or也能形成半环，它们也能映射到类型理论

这是更深刻的类比，也是逻辑与类型理论之间的 Curry-Howard 同构的基础

Kleisli范畴 / Kleisli Category

Kleisli Categories

<译> Kleisli 范畴

Kleisli 范畴给出了在范畴论中对副作用或非纯函数的进行构造或建模的方法。

从编程语言的视角，可以看作是将类型（目前所见都是返回类型）进行包装（包装的主要目的是加入一些附加信息），然后对包装后的类型的处理。态射就是从任意类型a到包装类型M b的函数a -> M b；态射复合 (>=>) :: (a -> M b) -> (b -> M c) -> (a -> M c) 该运算符称为"fish"；该范畴的恒等态射为 return :: a -> M a，举例如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

-- Writer in Haskell

type Writer a = (a, String)     -- 仅是在定义一个类型别名

-- 该范畴中的态射是从任意类型到Writer类型的函数 `a -> Writer b`
-- 复合的签名如下所示
(>=>) :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
-- 复合操作符的实现
m1 >=> m2 = \x ->
    let (y, s1) = m1 x
        (z, s2) = m2 y
    in  (z, s1 ++ s2)

-- 该范畴中的恒等态射
return :: a -> Writer a
return x = (x, "")

-- ----------------------
-- 对以上进行应用
-- 定义两个操作
upCase :: String -> Writer String       -- 将字符转换成大写，并带上附加信息
upCase = (map toUpper s, "upCase")
toWords :: String -> Writer [String]    -- 将字符串切成多个单词，并带上附加信息
toWords = (words s, "toWords")

toUpThenToWords :: String -> Writer [String]    -- 将以上两个操作复合起来
toUpThenToWords = upCase >=> toWords

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

// Writer in F#

type Writer<'a> = 'a * string   // 仅定义了类型别名

let (>=>) m1 m2 = fun x ->      // 这里推断为`m1:('a -> 'b * int) -> m2:('b -> 'c * int) -> x:'a -> 'c * int`
    let (y, s1) = m1 x
    let (z, s2) = m2 y
    (z, s1 + s2)

let toUpper str = Writer (str.ToUpper(), "toUpper") // 实际上没必要带上`Writer`
let toWords str = Writer (str.ToWords(), "toWords")

let proc = toUpper >=> toWords

// 可以将`Writer`声明为单实例的联合
type Writer<'a> = Writer of 'a * string
let (>=>) m1 m2 = fun x ->
    let (Writer (y, s1)) = m1 x
    let (Writer (z, s2)) = m2 y
    Writer (z, s1 + s2)

函子 / Functor

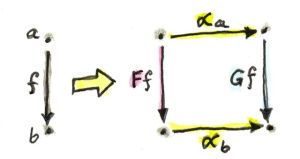
函子是范畴之间的映射，给定两个范畴C与D，函子可以将范畴C中的对象映射为D中的对象，将C中的态射映射为D中的态射并“保持结构”。若C中有一个对象a，它在D中的像即为F a；C中有一个态射f从对象a出发指向对象b，f在D中的像就是F f，它连接了a在D中的像与b在D中的像，如下图所示

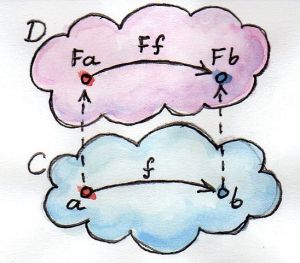
范畴结构中还包含态射复合及恒等态射。若在范畴C中有复合h = g . f，被函子F映射后，有F h = F g . F f；范畴C中对象a的恒等态射$id_a$被映射成范畴D中的$id_{F a}$，且$F id_a = id_{F a}$

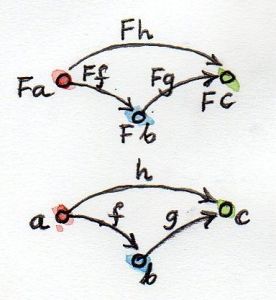
对函子的要求相对严格，因为要求函子保持范畴的结构，它可能会将一些对象“打碎”，也可能会将多个态射“合并”成一个，但它绝不会将任何东西丢弃掉，这种保持结构的约束类似于代数中的连续性条件，也就是说或函子具有“连续性”（函子的连续性还存在更多的限定概念）。

与函数类似，函子可以做折叠或嵌入的工作。所谓嵌入，就是将一个小的源范畴嵌入到更大的目标范畴中。一个极端的例子，源范畴是个单例范畴——只有一个对象与一个态射（恒等态射）的范畴，从单例范畴映射到任何其他范畴的函子，所做的工作就是在后者中选择一个对象。这完全类似于接受单例集合的态射，这个态射会从目标集合中选择元素。最巨大的折叠函子被称为常函子$\Delta_C$ ，它将源范畴中的每个对象映射为目标范畴中特定的对象c，也可以将源范畴中的每个态射映射为目标范畴中的特定的恒等态射，在行为上像一个黑洞，将所有东西压成一个奇点。

自函子 / Endofunctor

自函子是映射的目标范畴与源范畴相同的函子。

类型类 / Type Class

Haskell中使用类型类对函子进行抽象，一个类型类定义了支持一个公共接口的类型族。类型类是Haskell仅有的函数/运算符重载机制。

例如，定义支持相等谓词的类型类如下。该定义陈述的是，如果类型a支持(==)运算符，那么它就是Eq类。(==)运算符接受两个类型为a的值，返回Bool值。使用时声明某个特定类型是Eq族的一个“实例”，并提供(==)的实现，如下所示

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

-- 定义一个类型类
class Eq a where 
    (==) :: a -> a -> Bool

-- 定义某个类型
data Point = Pt Float Float

-- 声明该类型是Eq类型的实例，并给出相应实现
-- 注：在用到的`Point`的`Eq`功能时声明即可，不必在定义`Point`时声明
instance Eq Point where
    (Pt x y) == (Pt x' y') = x == x' && y == y'

函子类型类Functor定义如下：

1
2

class Functor f where
    fmap :: (a -> b) -> f a -> f b

这个类型类规定了：若存在符合以上签名的fmap方法，那么这个f是个函子。小写的f是个类型变量，类似于类型变量a与b，然而编译器能够推断出它是类型构造子而不是类型，依据是它的用途：它可作用于其他类型，即f a与f b。因此，要声明一个Functor的实例时，必须给出一个类型构造子，此处就是Maybe：

1
2
3

instance Functor Maybe where
    fmap _ Nothing = Nothing
    fmap f (Just x) = Just (f x)

F#不支持类型类，似乎仅能用静态类型解析进行约束，很麻烦很扯淡，此外需要新语言功能release才行（静态扩展允许作为类型解析的证据？）

编程中的函子

函子（这里仅关注编程中的自函子）不仅仅只映射对象（编程中对应物为类型），也映射态射（编程中对应物为函数）。

任意被其他类型参数化了的类型，都可视为候选函子。可将函子视为一个抽象的容器

Maybe函子

以Haskell中的Maybe为例，其定义data Maybe a = Nothing | Just a就是在将类型a映射为Maybe a。注意Maybe不是一个类型，是个类型构造子，需要提供一个类型参数如Int/Bool才能使之变成类型Maybe Int/Maybe Bool。对于任意函数f :: a -> b，Maybe函子需将之映射成f' :: Maybe a -> Maybe b，f'的实现为f' Nothing = Nothing及f' (Just x) = Just (f x)，即函数的参数是Nothing，那么返回Nothing即可；若这个函数的参数是Just，就将f应用于Just的内容。一般以高阶函数的形式来实现函子的态射映射部分，一般称fmap，例如对于Maybe函子，其fmap :: (a -> b) -> (Maybe a -> Maybe b)。通常说fmao“提升”/lift了一个函数，被提升的函数可以作用于Maybe层次上的值。由于Currying存在，对于fmap的签名(a -> b) -> Maybe a -> Maybe b有两个看待视角，一是接受一个a -> b类型的函数值，返回一个Maybe a -> Maybe b类型的函数值；另一个是接受一个a -> b类型的函数值和一个Maybe a类型的值，返回一个Maybe b类型的值。

为了证明类型构造子 Maybe 携同函数 fmap 共同形成一个函子，必须证明 fmap 能够维持恒等态射以及态射的复合。所证明的东西，叫做“函子定律”。凡是满足函子定律的函子，必定不会破坏范畴的结构。

F#及Scala中的对应物是Option，此外，F#中还有ValueOption

List函子

1
2
3
4
5

data List a = Nil | Cons a (List a)

instance Functor List where
    fmap _ Nil = Nil
    fmap f (Cons x t) = Cons (f x) (fmap f t)

List是类型构造子，将任意类型a映射为类型List a。为了证实List是一个函子，必须定义一个“提升”函数fmap :: (a -> b) -> (List a -> List b)，它接受一个a -> b函数，产生一个List a -> List b函数。

Reader 函子

Haskell中使用箭头类型构造子(->)构造函数类型。形如a -> b是对其的中缀使用形式，也可写作前缀形式(->) a b。该符合的偏应用/部分应用是合法的，例如(->) a是一个接受一个类型参数的类型构造子，它需要一个类型 b 来产生完整的类型 a -> b，它所表示的是，它定义了一族由a参数化的类型构造子。

可以将参数类型称为r，将返回类型称为a。因此类型构造子可以接受任意类型a，并将其映射为类型r -> a。为了证实这是个函子，需要一个提升函数fmap :: (a -> b) -> (r -> a) -> (r -> b)，它可以将函数a -> b“提升”为从r -> a到r -> b的函数，而r -> a与r -> b就是(->) r 这个类型构造子分别作用于a与b所产生的函数类型。对于给定的函数f :: a -> b与g :: r -> a，构造一个函数r -> b。复合两个函数是唯一途径，也恰恰就是当前所需。因此，fmap的实现为fmap f g = f . g，或者直接写作fmap = (.)

综上，类型构造子(->) r与这个fmap组合形成的函子便是Reader函子

1
2

instance Functor ((->) r) where
    fmap = (.)

Writer 函子

在Kleisli范畴中，态射是被“装饰”后的函数，返回的是一个type Writer a = (a, String)数据类型。这种“装饰”跟自函子有些关系，实际上Writer类型构造子对于a具备函子性。无需为之实现fmap，它只是个简单的积类型。

Kleisli范畴，定义了复合与恒等。复合是通过小鱼运算符实现的，恒等态射是一个叫做return的函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

-- composition
(>=>) :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
m1 >=> m2 = \x -> 
    let (y, s1) = m1 x
        (z, s2) = m2 y
    in (z, s1 ++ s2)

-- identity
return :: a -> Writer a
return x = (x, "")

基于以上两个函数，可以直接给出fmap :: (a -> b) -> (Writer a -> Writer b)的实现：fmap f = id >=> (\x -> return (f x))，这个fmap证实了Writer是个函子。注意实现里面小鱼运算符左侧id :: Writer a -> Writer a，这里(>=>) :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)并未约束a必须是个常规类型，它可以是任意类型，当然可以是个Writer b。因此fmap中的小鱼运算符接受了Writer a -> Writer a和a -> Writer b并最终返回了Writer a -> Writer b。

注意，以上是可以推广的：可以将Writer替换为任何一个类型构造子。只要这个类型构造子支持一个小鱼运算符以及 return，那就可以定义fmap。因此Kleisli范畴中的这种“装帧”，实际上是一个函子。（尽管并非每个函子都能产生一个 Kleisli 范畴）

这样定义的fmap否与编译器使用deriving Functor自动继承来的fmap是相同的。这是Haskell实现多态函数的方式所决定的。这种多态函数的实现方式叫做参数化多态，它是所谓的免费定理（Theorems for free）之源。这些免费的定理中有一个是这么说的，如果一个给定的类型构造子具有一个fmap的实现，它能维持恒等（将一个范畴中的恒等态射映射为另一个范畴中的恒等态射），那么它必定具备唯一性。

函子作为容器

Haskell模糊了数据与代码的区别。可以将列表视为函数，也可以将函数视为从存储着参数与结果的表中查询数据。如果函数的定义域有界并且不太大，将函数变成表查询是完全可行的。将函子对象（由自函子产生的类型的实例）视为包含着一个值或多个值的容器，即使这些值实际上并未出场；或者说函子对象可能包含产生这些值的方法，不必关心能否访问这些值——这些事发生在函子作用范围之外。如果函子对象包含的值能够被访问，就可以看到相应的操作结果；若不能被访问，那么所关心的只是操作的正确复合，以及伴随不改变任何事物的恒等函数的相关操作。

1
2
3
4

data Const c a = Const c

instance Functor (Const c) where
    fmap _ (Const v) = Const v

例如data Const c a = Const c，Const类型构造子接受两种类型， c与a，但它忽略参数a。类似之前处理箭头构造子那样，对其进行偏应用从而制造了一个函子。数据构造子（也叫Const）仅接受c类型的值，它不依赖a。与这种类型构造子相配的fmap类型为：fmap :: (a -> b) -> Const c a -> Const c b。因为这个函子是忽略类型参数的，所以fmap的实现可以忽略函数参数

函子的复合

函子的复合类似于集合之间的函数复合。两个函子的复合，就是两个函子分别对各自的对象进行映射的复合，对于态射也是这样。恒等态射穿过两个函子之后，它还是恒等态射。复合的态射穿过两个函子之后还是复合的态射。函子的复合只涉及这些东西。自函子很容易复合。

以MaybeTail :: [a] -> Maybe [a]为例，其实现MaybeTail [] = Nothing MaybeTail [x::xs] = Just xs，返回的结果是两个作用于a的函子Maybe与[]复合后的类型。这两个函子每个都有自己的fmap，若想将函数f作用于被Maybe []包含的内容，需要突破两层函子的封装。例如若要对mis :: Maybe [Int]中包含的数字mis = Just [1, 2, 3]用square x = x * x求平方，可以这样做：mis2 = fmap (fmap square) mis。经类型分析过后，对于内部的fmap使用List版本，外部的fmap使用Maybe版本。它可重写为mis2 = (fmap . fmap) square mis，重写版本是fmap :: (a -> b) -> (f a -> f b)视角，(fmap . fmap)中第二个fmap接受square :: Int -> Int返回[Int] -> [Int]，第一个fmap接受这个函数并返回Maybe [Int] -> Maybe [Int]，最终作用于mis并求得结果。两个函子的复合结果依然是函子，并且这个函子的 fmap是那两个函子对应的fmap的复合

函子的复合是遵守结合律的，因为对象的映射遵守结合律，态射的映射也遵守结合律。在每个范畴中也有一个恒等函子：它将每个对象都映射为其自身，将每个态射映射为其自身。因此在某个范畴中，函子具有与态射相同的性质。什么范畴会是这个样子？必须得有一个范畴，它包含的对象是范畴，它包含的态射是函子，也就是范畴的范畴。但是，所有范畴的范畴还必须包含它自身，这样我们就陷入了自相矛盾的境地，就像不可能存在集合的集合那样。但是，存在一个叫做 Cat 的范畴，它包含了所有的“小范畴”。这个范畴是一个“大的范畴”，因此它就不可能是它自身的成员。所谓的“小范畴”，就是它包含的对象可以形成一个集合，而不是某种比集合还大的东西。注意，在范畴论中，即使一个无限的不可数的集合也被认为是『小』的。以后也会看到函子也能形成范畴。

二元函子 / Bifunctor

函子是Cat范畴（范畴的范畴）中的态射，因此对于态射形成的直觉（编程中的函数）大部分可适用于函子。直觉上能理解一个函数接受两个参数，函子也可。接受两个参数的函子称为二元函子。对于对象而言，若一个对象来自范畴$C$，另一个对象来自范畴$D$，那么二元函子可以将这两个对象映射为范畴$E$中的某个对象。也就是说，二元函子是将范畴$C$与范畴$D$的笛卡尔积 $C \times D$映射为$E$，如下图所示。函子性也意味着二元函子也可以映射态射，也就是二元函子必须将一对态射（即范畴$C \times D$中的一个态射，其中一个来自$C$，一个来自$D$）映射为$E$中的一个态射。

注，若一个态射是在范畴的笛卡尔积中定义的，那么它的行为就是将一对对象映射为另一对对象。这样的态射可以复合(f, g) ∘ (f', g') = (f ∘ f', g ∘ g')，这样的复合是符合结合律的。此外，也有恒等态射(id, id)。范畴的笛卡尔积也是一个范畴。

将二元函子想象为具有两个参数的函数会更直观一些。要证明二元函子是否是函子，不必借助函子定律，只需独立的考察它的参数即可。如果有一个映射，它将两个范畴映射为第三个范畴，只需证明这个映射相对于每个参数（例如，让另一个参数变成常量）具有函子性，那么这个映射就自然是一个二元函子。对于态射，也可以这样来证明二元函子具有函子性。

个人理解：“二元函子”作为使“范畴的范畴”构成一个幺半群所需的二元运算。这需要联系幺半群定义去理解。

1
2
3
4
5
6
7

class Bifunctor f where
    bimap :: (a -> c) -> (b -> d) -> f a b -> f c d
    bimap g h = first g . second h      -- or: second h . first g
    first :: (a -> c) -> f a x -> f c x
    first g = bimap g id
    second :: (b -> d) -> f x b -> f x d
    second = bimap id

以上是用Haskell定义了一个二元函子，本例中，三个范畴都是Haskell类型范畴。一个二元函子是个类型构造子，它接受两个类型参数，类型变量f表示二元函子，关于它的所有应用都是在接受两个类型参数。二元函子伴随着一个“提升”函数bimap，它将两个函数映射为(f a b -> f c d)函数。bimap有一个默认的实现，即first与second的复合，这表明只要bimap分别对两个参数都具备函子性，就意味着它是一个二元函子(如下图)。

其他两个类型签名是first与second，他们分别作用于bimap的第一个与第二个参数，因此它们是f具有函子性的两个fmap证据(如下图)。上述类型类的定义以bimap的形式提供了first与second的默认实现。

当声明Bifunctor的一个实例时，可以去实现bimap，这样first与second就不用再实现了；也可以去实现first与 second，这样就不用再实现bimap。当然也可以三个都实现了，但是需要确定它们之间要满足类型类的定义中的那些关系。

积于余积二元函子 / Product and Coproduct Bifunctors

由泛构造定义的两个对象的积，即范畴积，是二元函子的一个重要例子。若任意两个对象之间存在积，那么从这些对象到积的映射便具备二元函子性。这通常是正确的，尤其是在Haskell中。

1
2

instance Bifunctor (,) where
    bimap f g (x, y) = (f x, g y)

序对构造子作为最简单的积类型，就是一个Bifunctor的实例。bimap :: (a -> c) -> (b -> d) -> (a, b) -> (c, d)作用是很清晰的。这个二元函子的用途就是产生的类型序对(,) a b = (a, b)

1
2
3

instance Bifunctor Either where
    bimap f _ (Left x) = Left (f x)
    bimap _ g (Right y) = Right (g y)

余积作为对偶，若它是作用于范畴内的每一对对象，那么它也是二元函子。以上给出了Haskell中余积二元函子Either的例子。

具备函子性的代数数据类型 / Functorial Algebraic Data Types

代数数据类型/ADT具备函子性。

目前所见的几个参数化数据类型的例子都是函子（可以为之定义fmap）。复杂的数据类型是由简单数据类型构造出来的，尤其是ADT，它是由和与积构造而来。目前以已确定积与和具备函子性及函子的复合，因此只需证实ADT的基本构造块具备函子性，那么就可以确定ADT基本函子性。

首先，有些构造块是不依赖于函子所接受的类型参数的，例如Maybe中的Nothing或者List中的Nil。它们等价与Const函子（Const函子忽略它的类型参数—实际上是忽略第二个类型参数，第一个被保留作为常量）。其次，有些构造块简单的将类型参数封装为自身的一部分，例如Maybe中的Just，它们等价于恒等函子。恒等函子是Cat范畴中的恒等态射，Haskell未对它进行定义，这里给出：

1
2
3

data Identity a = Identity a
instance Functor Identity where
    fmap f (Identity x) = Identity (f x)

可将Identity视为最简单的容器，它只存储类型a的一个（不变）的值。其他的代数数据结构都是使用这两种基本类型的和与积构建而成。

基于此来看待Maybe，data Maybe = Nothing | Just a。这是两种类型的和，求和是具备函子性的。第一部分Nothing可以表示为作用于类型a的Const ()（Const的第一个类型参数是unit），而第二部分不过是恒等函子的化名而已。在同构的意义下可以将Maybe定义为：type Maybe a = Either (Const () a) (Identity a)。Maybe是Const ()函子与Identity函子被二元函子Either复合后的结果。(Const本身也是一个二元函子，只不过在这里用的是它的偏应用形式)

两个函子的复合后，其结果是一个函子。此外，还需要确定两个函子被一个二元函子复合后如何作用于态射。对于给定的两个态射，可以分别用这两个函子对其进行提升，然后再用二元函子去提升这两个被提升后的态射所构成的序对。

可以在Haskell中定义这种复合 newtype BiComp bf fu gu a b = BiComp (bf (fu a) (gu b))，定义二元函子bf、两个函子fu与gu、两个常规类型a与b，将a应用到fu，b应用到gu，然后将fu a与gu b应用到bf。这是对象的复合，在Haskell中也是类型的复合。将Either、Const ()、Identity，a和b应用到BiComp得到的BiComp (Either (Const () a) (Identity b))，这就是一个裸奔版本的Maybe。

bf是二元函子、fu与gu是函子，那么这个新的数据类型BiComp就是a与b的二元函子。编译器必须知道与 bf 匹配的 bimap 的定义，以及分别与 fu 与 gu 匹配的 fmap 的定义。在 Haskell 中，这个条件可以预先给出：一个类约束集合后面尾随一个粗箭头：

1
2
3

instance (Bifunctor bf, Functor fu, Functor gu) =>
  Bifunctor (BiComp bf fu gu) where
    bimap f1 f2 (BiComp x) = BiComp ((bimap (fmap f1) (fmap f2)) x)

伴随BiComp的bimap实现是以伴随bf的bimap以及两个分别伴随fu和gu的fmap给出的。在使用bimap时，编译器会自动推断出所有类型，并选择正确的重载函数。bimap的定义中，x 的类型为bf (fu a) (gu b)，有点复杂。外围的bimap脱去它的bf层，然后两个fmap分别脱去它的fu与gu层。若f1 :: a -> a'及f2 :: b -> b'，那么，最终结果是类型 bf (fu a') (gu b')，因此bimap签名可以理解为bimap :: (fu a -> fu a') -> (gu b -> gu b') -> bf (fu a) (gu b) -> bf (fu a') (gu b')，这其实与bimap :: (a -> c) -> (b -> d) -> f a c -> f b d并无区别。

因此没有必要去证明Maybe是个函子，它是两个基本的函子求和后的结果，因此Maybe自然具备函子性。

对于代数数据类型而言，Functor实例的继承相当繁琐，这个过程可以由编译器自动完成。

1
2
3
4

{-# LANGUAGE DeriveFunctor #-}      -- 在代码首部启用Haskell扩展

data Maybe a = Nothing | Just a
  deriving Functor                  -- 声明该数据结构是个函子，然后就会得到相应的`fmap`的实现。

代数数据结构的规律性不仅适用于Functor的自动继承，也适合其它的类型类，例如之前提到的Eq类型类。也可以要求Haskell编译器自动继承自定义的类型类，但是技术上要难一点。不过思想是相同的：为类型类描述基本构造块、求和以及求积的行为，然后让编译器来描述其他部分。

协变与逆变函子 / Covariant and Contravariant Functor

回顾Reader函子，Reader函子(->) r是“函数箭头”类型构造子的的偏应用（箭头->本身就是一个类型构造子，它接受两个类型参数）。为之取一个类型别名，并将之声明为Functor实例

1
2
3
4

type Reader r a = r -> a

instance Functor (Reader r) where
    fmap f g = f . g

函数类型构造子接受两个类型参数，这一点与序对或Either类型构造子相似。序对与Either对于它们所接受的参数都具备函子性，因此它们二元函子。函数类型构造子是否是个二元函子？如果是，那么它必须对于两个类型参数都具备函子性，以上定义只给出了(->)对于它的第二个类型参数具备函子性，现在尝试证明对于第一个参数具备函子性。

需要固定第二个参数，使第一个参数可变，因此type Op r a = a -> r。此时对于Op r，返回类型r固定了下来，只让参数类型是a可变的。与它相匹配的fmap的类型签名如下：fmap :: (a -> b) -> (a -> r) -> (b -> r)。从fmap的类型签名看出，只凭借(a -> b)和(a -> r)类型的参数，无法构造出(b -> r)。但是如果存在某种方式能够反转a -> b，使之变成b -> a，那么目标构造便能成立。虽然不能随便反转一个函数的参数，但是在对偶范畴中可以这样做。

对于每个范畴$C$都存在一个对偶范畴$C^{OP}$，后者包含的对象与前者相同，后者包含的态射与前者一致但方向相反。假设范畴$C^{OP}$与另一个范畴$D$之间存在一个函子$F :: C^{OP} \rightarrow D$，这个函子将$C^{OP}$中的一个态射$f^{OP} :: a \rightarrow b$映射为$D$中的一个态射$F f^{OP} :: F a \rightarrow F b$。该态射$f^{OP}$与范畴$C$中的态射$f :: b \rightarrow a$相对应，两者方向是相反的。其形状如下图所示：

现在$F$是一个常规的函子，基于此定义一个映射$G$，该映射不是熟悉的普通函子。这个映射从范畴$C$到范畴$D$，映射对象时功能与$F$相同，映射态射时会先将态射方向反转，然后再使用$F$的功能。$G$接受$C$中的一个态射$f :: b \rightarrow a$，将其映射为相反的态射$f^{OP} :: a \rightarrow b$，然后将函子$F$作用于这个被反转的态射$f^{OP}$，最终得到$F f^{OP} :: F a \rightarrow F b$。$F a$与$G a$相同，$F b$与$G b$相同，因此$G f :: \lparen b \rightarrow a \rparen \rightarrow \lparen G a \rightarrow G b \rparen$。这种反转了态射方向的映射便称为“逆变函子”/Contravariant Functor。注意逆变函子只是来自对偶范畴的一个“常规函子”。之前所述的Maybe及List等都是“常规函子”，它们称为“协变函子”/Covariant Funcotr。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

-- Haskell中逆变函子类型类的定义 （实际是逆变自函子）
class Contravariant f where
    contramap :: (b -> a) -> f a -> f b

-- `Op`是它的一个实例
instance Contravariant (Op r) where
    -- contramap :: (b -> a) -> (a -> r) -> (b -> r)
    contramap f g = g . f  -- 函数 `f` 插入到了 `g` 之前

-- contramap 只是个颠倒了参数顺序的复合运算符
-- flip 函数可以用于颠倒参数顺序
flip :: (a -> b -> c) -> (b -> a -> c)
flip f y x = f x y
-- 基于此
contramap = flip (.)

副函子 / Profunctor

函数箭头运算符对于它的第一个参数具有逆变函子性，对于第二个参数具有协变函子性，在集合范畴Set中，这被称为副函子/Profunctor。由于一个逆变函子相当于其对偶范畴中的协变函子，因此可以这样定义一个副函子：$C^{OP} \times D \rightarrow Set$。

由于Haskell的类型系统可看作集合范畴，因此可以在其中定义副函子类型类。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

-- 从 Data.Profunctor 库中抽取出来的类型类
class Profunctor p where
    dimap :: (b -> a) -> (c -> d) -> p a c -> p b d
    dimap f g = lmap f . rmap g
    lmap :: (b -> a) -> p a x -> p b x
    lmap f = dimap f id
    rmap :: (c -> d) -> p x c -> p x d
    rmap = dimap id
-- 三个函数只是默认的实现。类似Bifunctor，当声明Profunctor实例时，要么实现dimap，要么实现lmap和rmap

-- 现在声明函数箭头运算符是Profunctor的实例
instance Profunctor (->) where
    dimap :: (b -> a) -> (c -> d) -> (a -> c) -> (b -> d)
    dimap ba cd ac = cd . ac . ba
    lmap = flip (.)
    rmap = (.)

函数类型 / Function Type

构造函数类型

尝试运用泛构造的知识构造一个函数类型，或者从广义上说，构造一个内hom-集。

可将函数类型视为一种复合类型，因为它描述的是一个参数类型和结果类型之间的关系。积类型和余积类型便是复合类型的泛构造，这里运用同样的技巧。

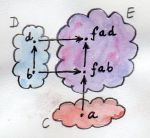
首先给出对象及联系对象的模式。这里有三个对象：要构造的函数类型、参数类型和返回类型。显然，联系这三者的模式就是函数应用或求值。对于函数类型，假设存在一个候选者z(在非集合范畴中，z只是个普通对象)，设参数类型为a(一个对象)，函数应用可将z与a构成的序对映射为结果类型b(一个对象)。现在可以认为已有三个对象了，其中两个已固定(参数类型和返回类型)，另一个是“应用”。“应用”是一种映射，若能查看对象内部，那么可以将一个函数f(z的一个元素)与参数x(a的一个元素)封装为序对，然后将这个序对映射为f x(f作用于x，结果是b的一个元素）只处理单个的序对(f, x)并无太大价值，要处理的是函数类型的候选者z与参数类型a的积，即z × a。这个积是一个对象，可以选择从这个对象到b的一个箭头g作为态射，g也就是“应用”。在集合的范畴中，g就是将每个(f, x)映射为f x的函数。这样就建立起了这样一个模式：对象z与对象a的积，通过态射g被关联到另一个对象b。

要利用泛构造技巧来清晰的刻画函数类型，这样的模式够用么？这个模式不适于所有范畴，但是对于我们感兴趣的那些范畴，它够用了。还有一个问题：定义一个函数类型，必须事先定义积类型吗？有些范畴是不可积的，或者并非所有成对的对象都能构成积。这个问题的答案是不行，如果没有积类型，就没有函数类型。

以上构造通常会命中很多东西，它们都符合这个模式。特别是在集合的范畴中，几乎每一样东西都与其他东西具有相关性。可以选取任意一个对象z，将其与a形成积，再找个函数将积映射为b（除非b是空集）。因此需要建立排序机制并找出最好的那个。当且仅当存在一个唯一的从z'到z的映射，使得g'可由g来构造，即可判定伴随态射g(从z×a到b)的z比伴随g'的候选者z'更好。如下图所示

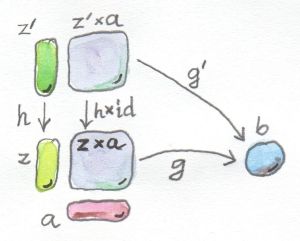
假设存在态射h:: z' -> z，想获得从z' × a到z × a的态射。由于积类型具备函子性，或者说积类型本身是个函子(更确切的说，是二元自函子)，因此可以提升一对态射。也就是说不仅能定义对象的积，也能定义态射的积。不需要改变z' × a这个积的第二个成员，因此要提升的态射序对是(h, id)，其中id是作用于a的恒等态射。现在有g' = g ∘ (h × id)。

泛构造的第三个步就是选出最好的那个候选者，将之称为a⇒b(在这里，将它视为一个对象的名字即可，不要与 Haskell 类型类的约束符号混淆，下文会给出其他命名方式)。这个对象伴随的“应用”称为eval，即eval :: (a⇒b) × a -> b。若其他候选者所对应的“应用”g都能由eval唯一的构造出来，那么a⇒b就是最好的那个候选者。

其形式定义如下：

一个从a到b的函数对象是伴随着态射eval :: ((a⇒b) × a) -> b的a⇒b，它对于伴随着态射g :: z × a -> b的任意其它对象z而言，存在唯一的态射h :: z -> (a⇒b)，使得g = eval ∘ (h × id)。

不能确保对于某个范畴中的任意的对象a与b都存在着a⇒b，但是对于集合的范畴却总是存在着这样的a⇒b，并且在集合的范畴中a⇒b与Hom-集**Set(a,b)**同构。这也是在Haskell中将函数类型a -> b解释为范畴意义上的函数对象a⇒b的原因。

柯里化 / Curring

“接受两个参数的函数”与“接受一个参数并返回函数的函数”存在一一对应的关系，这种对应关系叫做柯里化

再次观察函数类型的所有候选者，这次将态射g视为接受两个参数的函数g :: z x a -> b(一个接受积类型的态射与一个接受两个变量的函数很相似，尤其是在集合范畴中，g是接受值的序对的函数，其中一个值来自集合z、另一个来自集合a)；另一方面，基于泛性质，可以知道对于每个这样的g都存在唯一的态射h能将z映射为函数类型a⇒b，即h :: z -> (a⇒b)。在集合范畴中，这意味着h是一个接受z类型参数并返回一个从a到b的函数的函数，h是一个高阶函数。这种泛构造在“接受两个参数的函数”与“接受一个参数并返回函数的函数”建立的一一对应的关系，这种对应关系叫做柯里化，且h称为g的柯里化版本。

这种关系是一一对应的。对于任意函数g都存在唯一的h，而对于任意的h也总是能重加一个接受两个参数的函数g，且g = eval ∘ (h × id)。可以将g称h的反柯里化版本。

柯里化是Haskell和F#内置的语法，返回一个函数的函数a -> (b -> c)可直接视为一个接受两个参数的函数a -> b -> c，这样能直接支持函数的部分应用(即先只给出一个参数，产生一个接受单一参数的函数)。Scala不直接支持这一概念，需要显式定义多参数列表的方法def f[A,B,C](a: A)(b: B): C = ???，这种函数才能支持部分应用

严格将，接受两个参数的函数，其本质接受的是一个序对/积类型，即(a, b) -> c，这也一般是函数式编程语言与面向对象编程语言交互时看待“对象方法”的方式。但是两种形式的转换一般很容易

1
2
3
4
5
6

-- Haskell似乎内置了一下两个函数
curry :: ((a, b)->c) -> (a->b->c)
curry f a b = f (a, b)

uncurry :: (a->b->c) -> ((a, b)->c)
uncurry f (a, b) = f a b

1
2
3

// F# 中似乎没有内置，但是也很容易就能实现出来
let curry f a b = f (a, b)
let uncurry f (a, b) = f a b

指数 / Exponential

在数学领域，从对象$a$到对象$b$的函数或内hom-对象(内hom-集中的对象)通常称为指数，表示为$b^a$。注意，函数参数类型位于指数的位置。

上文构造函数类型时提到了必须借助积才行，然而函数与积还有更深层的联系。考虑建立在有限类型(即值的数量为有限的类型，例如Bool、Char甚至Int、Double等)上的函数，理论上，这种函数是“可记忆”的，可将这些函数运算转换成查表操作，这也是函数(态射)与函数类型(对象)之间等价的本质。例如，一个接受Bool的纯函数可以被特化为一对值，一个对应于True另一个对应于False。那么，所有从Int到Bool的函数等价于所有Int序对构成的集合，用积来表示就是Int x Int，或者$Int^2$，即$Int^{Bool}$

实践中并不会要求一个接受Int或Double的函数做成查表实现，因为这样不切实际。但应当承认函数与数据类型之间的等价性确实存在。Haskell是个惰性求值的语言，在惰性求值的（无限的）数据结构与函数之间的界限并不那么明显。这种函数与数据之间的对偶性揭示了Haskell的函数类型与范畴化的指数对象之间的等价性。

指数与代数数据类型

从指数的角度来阐释函数类型，这种方式也能很好的适用于代数数据类型。事实上，中学代数中所涉及的0、1、加法、乘法以及指数等结构，在任何双向笛卡尔闭范畴中同样存在，它们分别对应于初始对象、终端对象、余积、积以及指数等。现在还没有足够的工具（诸如伴随（Adjunction）或 Yoneda 定理）来证明这一点，不过在此可以直观呈现。

0次幂 $a^0 = 1$

在范畴论中，0即初始对象，1即终端对象，“相等”即恒等态射，指数即内hom-对象。这个特殊的指数表示的是从初始对象到任意对象$a$的态射集合。基于初始对象的定义，这样的态射只有一个，因此hom-集$C(0,a)$是一个单例集合。一个单例集合在集合范畴中是终端对象，因此上面这个等式在集合范畴中是成立的，这也意味着它在任何双向笛卡尔闭范畴中都成立。

Haskell中用Void表示0，用unit类型()表示1，用函数类型表示指数。所有从Void到任意类型a的函数集合等价于unit类型，即单例集合。换句话说，有且仅有一个函数Void -> a，这个函数之前提到过，叫做absurd。注意，这样解释存在一些漏洞，原因有二。首先，Haskell中不存在没有值的类型，每种类型都包含着“永不休止的运算”，即底；此外，absurd的所有实现都是等价的，无论如何实现，都不可能对其进行调用，因为没有值可以传递给absurd（如果传递给它一个永不休止的运算，它永远也不会返回结果）

1的幂 $1^a = 1$

在集合范畴中，这个等式重申了终端对象的定义：从任意对象到终端对象存在唯一的态射。从a到终端对象的内hom-对象通常与终端对象本身是同构的。

在Haskell中，只有一个函数是从任意类型a到unit类型的，这个函数叫unit，也可以认为它是const函数对()的偏应用。

1次幂 $a^1 = a$

这个等式重申了从终端对象出发的态射可用于从对象a中拮取元素。这种态射的集合与对象a本身是同构的。在集合范畴与 Haskell中，集合a与从a中拮取元素的函数() -> a是同构的。

指数的和 $a^{b + c} = a^b \times a^c$

从范畴论的角度来看，这个等式描述的幂为两个对象的余积的指数与两个指数的积同构。

在Haskell中这种代数等式的解释是：两个类型的和的函数与两个参数类型为单一类型的函数的积同构。这恰恰就是在定义作用于和类型的函数时所用到的分支分析，也就是说，函数定义中的case语句可以用两个或多个处理特定类型的函数来替代。例如，下面这个从和类型(Eigher Int Double)出发的函数f :: Either Int Double -> String 可以定义为一个函数对：

1
2
3

f (Left n)  = if n < 0 then "Negative int" else "Positive int"
f (Right x) = if x < 0.0 then "Negative double" else "Positive double"
-- 在此，`n` 是 `Int`，而 `x` 是 `Double`。

指数的指数 $(a^b)^c = a^{b \times c}$

这个等式表达的是指数对象形式的柯里化，即返回一个函数的函数等价与积类型的函数（带两个参数的函数）。

积的指数 $(a \times b)^c = a^c \times b^c$

在Haskell中，返回一个序对的函数与一对函数等价，后者的每个函数都返回序对的一个元素。

笛卡尔闭范畴 / Cartesian Closed Category

包含终端对象、任意对象序对的积以及任意对象序对的指数的范畴是笛卡尔闭范畴。集合范畴就属于此类范畴。

将指数看作重复的积（可能是无限次），那就可以将笛卡尔闭范畴视为支持任意数量的积运算的范畴。特别地，可将终端对象视为0个对象的积，或者一个对象的0次幂。从计算机科学的角度来看，笛卡尔闭范畴为简单的类型Lambda演算（类型化的编程语言的基础）提供了模型。

终端对象与积也分别具有对偶物：初始对象与余积。笛卡尔闭范畴也支持这两者，积通过分配率可转化为余积：a × (b + c) = a × b + a × c (b + c) × a = b × a + c × a。这样的范畴被称为双向笛卡尔闭范畴。

柯里-霍华德同构 / Curry-Howard Isomorphism

逻辑学与代数数据类型之间有一些对应关系。Void类型与unit类型()分别对应于错误与正确；积类型与和类型分别对应于逻辑与运算$\vee$与逻辑或运算$\wedge$。遵循这一模式，函数类型对应于逻辑推理$\Longrightarrow$，换句话说，类型a -> b可以读为“如果 a 那么 b”。

根据柯里-霍华德同构理论，每种类型皆可视为一个命题，它们是为真或为假的陈述语句。如果类型是有值的，那么它就是真命题，否则就是伪命题。在实践中，如果一个函数类型有值，亦即存在这样的函数，那么与它对应的逻辑推理就为真。去实现一个函数，就是在证明一个定理。写程序，就等价于证明许多定理。

以函数类型定义中所用的eval函数为例，它的签名是：eval :: ((a -> b), a) -> b。它接受一个由函数与其参数构成的序对，产生相应的类型。这个函数是一个态射的Haskell实现，该态射为：eval :: (a⇒b) × a -> b。这个态射定义了函数类型a⇒b（或指数类型$b^a$）。运用柯里-霍华德同构理论，可将这个签名转化为逻辑命题：$((a \Longrightarrow b) \vee a ) \Longrightarrow b$ 可将上面这条陈述读为：如果b由a推出为真，且a为真，那么b肯定为真。这就是所谓的肯定前件式。要证明这个定理，只需要实现一个函数，即eval :: ((a -> b), a) -> b eval (f, x) = f x。如果有一个从a到b的函数f以及a类型的一个值x所构成的序对，就可以将f作用于x，从而产生b类型的一个值。通过实现这个函数，可以证明((a -> b), a) -> b是有值的。因此，在该逻辑中，这一肯定前件式为真。

再给出一个结果为假的逻辑命题。看这个例子，如果a或b为真，那么a肯定为真：$a \wedge b \Longrightarrow b$。这个命题肯定是错的，因为当a为假而b为真时，就可以构成一个反例。运用柯里-霍华德同构理论，可将这个命题映射为函数签名：Either a b -> a，根本无法实现这样的函数，因为对于Right构造的值而言，无法产生类型为a的值（注：仅限纯函数）

最后，重新理解absurd :: Void -> a。将Void视为假，可得：$false \Longrightarrow a$，这意味着由谎言可推理出一切（爆炸原理）。对于这个命题（函数），下面用 Haskell 给出的一个证据（实现）：absurd (Void a) = absurd a 其中Void的定义如下：newtype Void = Void Void 这是惯用的花招，这个定义使得Void不可能用于构造一个值，因为要用它构造一个值，前提是必须先提供这个类型的一个值，这样就使得absurd永远无法被调用

自然变换 / Natural Transformation

自然变换是保持函子性质不变的特殊映射，它是函子之间的映射。

函子可以在维持范畴结构的前提下实现范畴之间的映射。函子可以将一个范畴嵌入到另一个范畴，也可以让多个范畴坍缩为一个范畴且不会破坏范畴的结构，甚至可以在一个范畴之内构建另一个范畴。源范畴可视为目标范畴的部分结构的模型或蓝图。将一个范畴嵌入到另一个范畴可能有许多种方式，这些方式有时是等价的，有时不等价。可以将整个的范畴坍缩为另一个范畴中的一个对象，也可以将一个范畴中的每个对象映射为另一个范畴中不同的对象，并将前者中的每个态射映射为后者中的不同的态射。同样的想法可以有多种不同方式的实现。自然变换可以用于对比这些实现。

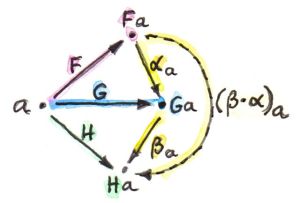
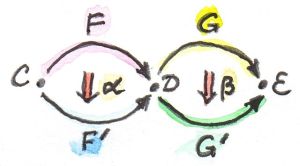
对于范畴$C$与$D$之间的两个函子$F$与$G$，若只关注$C$中的一个对象$a$，它被映射为$D$中的两个对象：$F a$和$G a$，那么应该存在一个函子映射$\alpha_a$，它可以将$F a$映射为$G a$，如下图所示

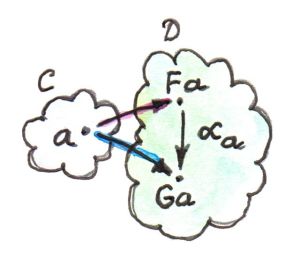
由于在同一范畴中的对象映射应该不会脱离该范畴，因此不想再额外建立$F a$和$G a$的联系，因此很自然地考虑使用现有态射。自然变换本质上是如何选取态射：对于任意对象$a$，自然变换就是选取一个从$F a$到$G a$的态射。若将一个自然变换称为$\alpha$，那么这个态射就称为在$a$上的$\alpha$分量(Component of $\alpha$ at $a$)，记作$\alpha_a$。注：$\alpha_a :: F a \rightarrow G a$，此外$a$是一个在$C$中的对象，而$\alpha_a$是$D$中的一个态射。对于某个$a$，若在$F a$与$G a$之间没有态射，那么$F$与$G$之间也就不存在自然变换。

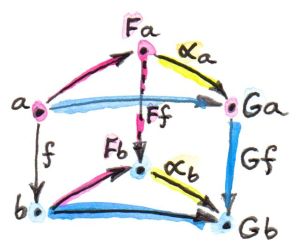
函子映射的不只是对象，它也能映射态射，而自然变换对态射的映射是固定的，在两函子$F$与$G$之间的任意自然变换下，$F f$必须映射到$G f$。如下图所示，范畴$C$中两个对象$a$与$b$之间的态射$f$，被映射为范畴$D$中的两个态射$F f :: F a \rightarrow F b$和$G f :: G a \rightarrow G b$。自然变换$\alpha$提供了两个态射(即为$\alpha$在$a$及$b$上的两个分量，$\alpha_a :: F a \rightarrow G a$和$\alpha_b :: F b \rightarrow G b$)补全了$D$中的结构。为保证两个从$F a$到$G b$的途径是等价的，必须要引入自然性条件/Naturality Condition：$G f \circ \alpha_a = \alpha_b \circ F f$

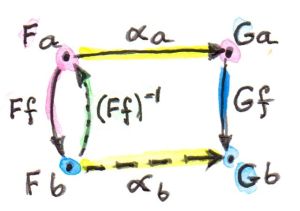
自然性条件对于任意态射$f$都成立。若态射$F f$是可逆的，基于自然性条件能给出$\alpha_b = G f \circ \alpha_a \circ (F f)^{-1}$(即$\alpha_a$表示的$\alpha_b$)，如下图所示。若两个对象之间存在多个可逆的态射，上述变换也都成立。尽管态射通常是不可逆的，两个函子之间的自然变换也并非一定存在。与自然变换相关的函子的多寡，可在很大程度上显现这些函子所操纵的范畴的结构。

从分量的角度看待自然变换，可以认为自然变换$\alpha$将范畴$C$中的对象$a$映射为范畴$D$中的态射$\alpha_a$；从自然性角度来看，可认为自然变换将态射$f$映射为一个正方形交换图，如下所示。自然变换的这一性质可以让很多范畴便于构造，这些范畴往往包含着这类的交换图。在正确选择函子的情况下，大量的交换条件都能够转换为自然性条件。

自然变换可用于定义函子的同构。若自然变换的各个分量都是同构的（态射可逆），那么这两个函子自然同构。若两个函子是自然同构，差不多是在说它们是相同的函子。

多态函数 / Polymorphic Function

函子（确切地说是自函子）在编程中有广泛应用，它能将类型映射为类型（其自身具备类型构造子功能），也能将函数映射为函数（借助高阶函数fmap实现）

假定存在函子F可将类型a映射为F a和函子G可将类型a映射为G a，在a上的自然变换的alpha分量是一个从F a到G a的函数alpha_a :: F a -> G a。自然变换alpha是面向所有类型a的多态函数alpha :: forall a . F a -> G a（forall a在Haskell中是可选功能，可以用语言扩展ExplicitForAll开启，通常可将其写为alpha :: F a -> G a），这是一个由a参数化的函数族。C++中与之类似的构造有些复杂template<Class A> G<A> alpha(F<A>);

Haskell的多态函数与C++的泛型函数之间存在很大的区别，主要体现为函数的实现方式以及类型检查方式上。Haskell中，一个多态函数必须对于所有类型是唯一的，一个公式必须适用于所有的类型，这是所谓的参数化多态/Parametric polymorphism；C++默认提供的是特设多态/Ad hoc polymorphism，这意味着模板不一定涵盖所有类型，一份模板是否适用于某种给定的类型需要在实例化时方能确定，彼时编译器会用一种具体的类型来替换模板的类型参数，类型检测是以推导的形式实现的，因此编译器经常会给出难以理解的错误信息。在C++中，还有一种函数重载与模板特化机制，通过这种机制可以为不同的类型定义函数的不同版本。Haskell有类似的机制，即类型类（Type class）与类型族（Type family）

Haskell中这种类型的多态函数alpha :: F a -> G a，函子F与G自动满足自然性条件（即$G f \circ \alpha_a = \alpha_b \circ F f$）。Haskell中函子G作用于一个态射f是通过fmap实现的，可表示为fmap_G f . alphaa = alphab . fmap_F f，Haskell的类型推导十分强大，类型标记是不需要的，因此可写为fmap f . alpha = alpha . fmap f。这不是真正的Haskell代码（在代码中无法表示函数等式），但它给出了恒等，在等式推导中可以使用这个公式，编译器也可以利用这个公式对代码进行优化。

之所以在Haskell里自动满足自然性条件，这是“免费定理”的自然结果。Haskell里，将参数化多态用于定义自然变换，会引入非常强的限制条件：一个公式必须适应所有类型。这些限制条件会变成面向这些函数的方程一样的定理。对于能够对函子进行变换的函数，免费的定理是自然性条件。

在Haskell中，函子可以视为泛型容器，继续这个类比，自然变换只是一个重组方式，将一个容器中的东西取出来放到零一个容器里，自然变换不触碰这些东西。于是，自然性条件就体现为：这个重组方式不关心我们是先通过fmap修改这些东西，然后再将它们放到新容器里，还是先放到新容器里再用适用于新容器的fmap去修改它们，重组与fmap是正交的。

下面给出几个例子

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

-- `List`与`Maybe`函子之间的自然变换`safeHead`
safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:xs) = Just x

-- 它需要满足的自然性条件：
fmap f . safeHead = safeHead . fmap f

-- 用`fmap`对其进行验证
fmap :: (a -> b) -> f a -> f b
-- `List`函子的`fmap`
fmap f [] = []
fmap f (x:xs) = f x : fmap f xs
-- `Maybe`函子的`fmap`
fmap f Nothing = Nothing
fmap f (Just x) = Just (f x)

-- 空列表
fmap f . (safeHead []) = fmap f Nothing = Nothing
safeHead (fmap f []) = safeHead [] = Nothing

-- 非空列表
fmap f (safeHead (x:xs)) = fmap f (Just x) = Just (f x)
safeHead (fmap f (x:xs)) = safeHead (f x : fmap f xs) = Just (f x)

以上是个常见的自然变换的样子。但一个以Const函子为始点或终点的自然变换，看上去就像一个函数，它既面向它的返回类型多态，也面向它的参数类型多态。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

-- `length`视为从列表函子到`Const Int`函子的自然变换：
length :: [a] -> Const Int a
length [] = Const 0
length (x:xs) = Const (1 + unConst (length xs))

-- `unConst`用于剥除`Const`构造子
unConst :: Const c a -> c
unConst (Const x) = x

-- 实际上`length`的定义：
length :: [a] -> Int
-- 这个定义有效地掩盖了`length`作为自然变换的本质

-------------------------------------

-- 寻找一个以`Const`函子为始点的参数化多态函数有点难，因为这需要无中生有创造一个值出来。能想到的最好办法是：
scam :: Const Int a -> Maybe a
scam (Const x) = Nothing

还有一个不同寻常的函子，它在Yoneda引理中扮演了重要的角色，这个函子就是Reader函子

1
2
3
4

-- 这个函子被两种类型参数化，仅第二个类型具备协变函子性：
newtype Reader e a = Reader (e -> a)
instance Functor (Reader e) where
    fmap f (Reader g) = Reader (\x -> f (g x))

对于每种类型e，都可以定义从Reader e到任何其他函子f的自然变换族，这个家族的成员总是与f e的元素一一对应（Yoneda引理）。考虑仅有一个值()的类型unit，函子Reader ()接受任意类型a，然后形成函数类型() -> a，这些函数可以从集合a中提取一个元素，函数的数量与a中的元素一样多。考虑该函子到Maybe函子的自然变换alpha :: Reader () a -> Maybe a，这样的自然变换只有dumb（dumb (Reader _) = Nothing）和obivous（obvoius = (Reader g) = Just (g ())）。实际上按照 Yoneda 引理的说法，这与Maybe ()类型的两个元素相符，即 Nothing 与 Just ()（注意该说法并不严谨）

超自然性 / Beyond Naturality

两个函子之间的参数化多态函数（包括Const函子这种边界情况）必定是自然变换。因为所有的标准代数数据类型都是函子，在这些类型之间的任何一个多态函数都是自然变换。函数类型的返回类型具备函子性，可以运用这一特点来构造函子（例如Reader函子），并为这些函子构造自然变换，这些自然变换是更高阶的函数。

但是，函数类型的参数类型具备的是逆变函子性（逆变函子就是对偶范畴中的协变函子）。在范畴意义上，两个逆变函子之间的多态函数依然可视为自然变换，当然它们只能作用于Haskell类型范畴的对偶范畴里的函子。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

-- 逆变函子`Op`对于`a`具有逆变性
newtype Op r a = Op (a -> r)
instance Contravariant (Op r) where
    -- contramap :: (b -> a) -> (Op r a -> Op r b)
    -- contramap :: (b -> a) -> (a -> r) -> (b -> r)
    contramap f (Op g) = Op (g . f)

-- 一个从`Op Bool`到`Op String`的函数
predToStr (Op f) = Op (\x -> if f x then "T" else "F")
-- 函子`Op Bool`和`Op String`不具备协变性，它们不是**Hask**范畴中的自然变换。但它们具备逆变性，因此满足“相反的”自然性条件：
contramap f . predToStr = predToStr . contramap f
-- 注：函数`f`必须走与`fmap`作用下方向相反的方向

存在不是函子的类型构造子，例如a -> a。类型参数a出现在负（逆变）位与正（协变）位上，对于这种类型，fmap或contramap都无法实现。符合函数签名(a -> a) -> f a（其中f是任意函子）的函数不是自然变换。存在着一种广义的自然变换，叫作双自然变换，它们能够处理这些情况。

函子范畴 / Functor Category

对于每对范畴$C$和范畴$D$，存在且仅存在一个函子范畴，在这个范畴里，对象是从$C$到$D$的函子，态射是函子间的自然变换。对于每个函子$F$，存在一个恒等自然变换$1_F$，它的分量恒等态射$id_{F a} :: F a -> F a$；已知自然变换的分量是态射，自然变换的复合就是各分量态射的复合，态射复合遵循结合律，因此自然变换复合也遵循结合律。

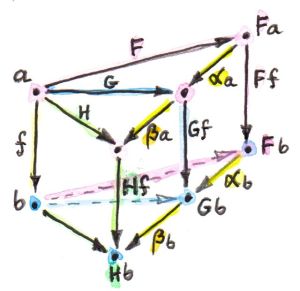
例如，现有函子$F$到函子$G$的自然变换$\alpha$和函子$G$到函子$H$的自然变换$\beta$，它们在对象$a$上的分量是某个态射$\alpha_a :: F a \rightarrow G a$和$\beta_a :: G a \rightarrow H a$，这两个态射是可以复合的，复合结果是另一个态射$\beta_a \circ \alpha_a :: F a \rightarrow H a$，可以将这个结果作为自然变换$\beta \cdot \alpha$（自然变换$\alpha$和$\beta$的复合，复合顺序先$\alpha$后$\beta$）在$a$上的分量，即$(\beta \cdot \alpha)_a = \beta_a \circ \alpha_a$(如下图所示)

复合后的自然变换依然满足自然性条件$H f \circ (\beta \cdot \alpha)_a = (\beta \cdot \alpha)_b \circ H f$，如下图所示

关于自然变换复合的记法

以上的给出的示意图里面，函子是从上向下堆砌的，这种称为竖向复合，用小圆点$\cdot$来表示。此外还有横向复合，用小圆圈$\circ$表示，有时可能是星号。

范畴$C$与范畴$D$之间的函子范畴记作$Func(C, D)$或$[C, D]$，有时也记作$D^C$。最后这种记法暗示了可将函子范畴本身视为一个其它范畴中的函数对象（指数）

范畴由对象和态射构成；范畴（严格来讲是小范畴，它们的对象形成集合）本身是更高层范畴Cat中的对象，Cat中的态射是函子；Cat里的Hom-集是函子构成的集合。例如$Cat(C,D)$是范畴$C$与$D$之间的函子集合，函子范畴$[C, D]$也是两个范畴间的函子集合（自然变换作为态射），$[C, D]$中的对象也就是$Cat(C,D)$集合中的东西。此外，函子范畴自身也是范畴，它也是Cat中的对象之一（也就是说，两个小范畴之间的函子范畴本身也很小）。一个范畴里的Hom-集与同一个范畴里的对象之间存在联系（即内hom-集），这种情况就类似之前看到的指数形式的对象

为构造一个指数，首先要定义积。在Cat里，定义积相当容易。小范畴是对象的集合，集合之上可以定义笛卡尔积，积范畴$C \times D$中的一个对象，是两对象构成的序对$(c, d)$（一个来自范畴$C$，一个来自范畴$D$）；类似地，$(c, d)$与$(c', d')$之间的态射是一个态射序对$(f, g)$，其中$f :: c \rightarrow c'$、$g :: d \rightarrow d'$；态射序对由来自两范畴的态射构成，总会有一个分别由两范畴的恒等态射构成的序对。Cat是一个完全的笛卡尔闭范畴，对于任意一对范畴$C$和$D$，它里面存在着相应的指数对象$D^C$。Cat里的对象是范畴的，因此$D^C$是范畴，它就是范畴$C$与$D$之间的函子范畴

2-Categories / 2-范畴

2-范畴是一个广义的范畴，其中具备对象和态射（准确讲，应该是1-态射），还有2-态射（即态射之间的态射）。

按照定义，Cat里任意Hom-集都是函子集合，其中两对象之间的函子形成一个函子范畴，函子范畴中以自然变换作为态射。在Cat里，对象是（小）范畴，函子是对象间的态射，自然变换就是态射间的态射。这个更“丰满”的结构便是2-范畴的一个例子。

用函子范畴$D^C$的形式来代替范畴$C$和$D$之间的Hom-集。现有常规的函子符合：来自$D^C$的函子$F$与来自$E^D$的函子$G$复合，可以得到来自$E^C$的函子$G \circ F$。此外，在每个Hom-范畴内部，也存在着复合，这就是函子之间的自然变换或2-态射的竖向复合，如下图所示。

要分析清楚这两种复合之间关系，首先从Cat里面选两个函子（或者说1-态射）$F :: C \rightarrow D$和$G :: D \rightarrow E$，以及它们的复合$G \circ F :: C \rightarrow E$，此外还有两个自然变换$\alpha :: F \rightarrow F'$和$\beta :: G \rightarrow G'$，整体关系如下图。显然，不可能对两个自然变换应用竖向复合，因为$\alpha$的终点与$\beta$起点不重合（实际上因为它们属于两个函子范畴$D^C$和$E^D$）。

基于以上条件，很明显可以复合函子$F'$和$G'$得到$G' \circ F'$。现在尝试基于已有的$\alpha$和$\beta$定义一个从$G \circ F$到$G' \circ F'$的自然变换。首先给出简图如下

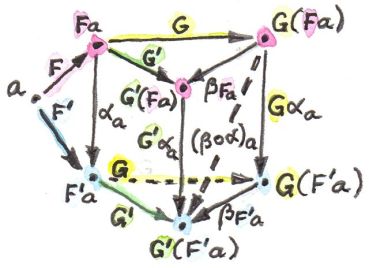
从范畴$C$中的一个对象$a$开始，它分裂为$D$中的两个对象$F' a$和$F' a$，此外有一个态射$\alpha_a :: F a \rightarrow F' a$连接这两个对象，这个态射是$\alpha$的分量；在从$D$到$E$的时候，两个对象分裂成四个对象$G (F a)$、$G' (F a)$、$G (F' a)$和$G' (F' a)$，还有四个态射形成了一个方格，其中有两个是$\beta$的分量：$\beta_{F a} :: G (F a) \rightarrow G' (F a)$和$\beta_{F' a} :: G (F' a) \rightarrow G' (F' a)$，另两个是$\alpha_a$在两个函子下的象（函子提升了的态射）：$G \alpha_a :: G (F a) \rightarrow G (F' a)$和$G' \alpha_a :: G' (F a) \rightarrow G' (F' a)$。目标是从中找出$G (F a)$到$G' (F' a)$的态射，找到了$G' \alpha_a \circ \beta_{F a}$和$\beta_{F' a} \circ G \alpha_a$，这两者是相等的。这四个态射形成的方格对于$\beta$而言具备自然性。将这个自然变换称为$\alpha$与$\beta$的横向复合：$\beta \circ \alpha :: G \circ F \rightarrow G' \circ F'$

复合的存在依赖于范畴。自然变换的纵向符合存在于函子范畴，现找出横向复合存在的范畴。解决这个问题需要从侧面来看Cat，不要将自然变换看成函子之间的态射，而是将它们看成范畴之间的态射。一个自然变换位于两个范畴之间，而这两个范畴原本是由这个自然变换所变换的函子连接的，可以认为这个自然变换连接着这两个范畴。从Cat里面选择两个对象，即范畴$C$和$D$，两对象之间存在着由自然变换构成的集合，这些自然变换来往于连接$C$和$D$的函子之间，将这些自然变换视为从$C$到$D$的态射。同理，也有一些自然变换是来自于连接范畴$D$和$E$的函子，将它们视为从$D$到$E$的态射。于是，横向复合就是这种态射的复合。存在从范畴$C$到范畴$C$的恒等态射，它是范畴$C$上恒等函子自身的恒等自然变换。注：横向复合的恒等也是竖向复合的恒等，但反过来不是。

横向复合和纵向复合满足交换律：$(\beta' \cdot \alpha') \circ (\beta \cdot \alpha) = (\beta' \circ \beta) \cdot (\alpha' \circ \alpha)$。

此后可能会看到更多记法。在从侧面看待Cat的视角里，从一个对象到另一个对象有两种办法：使用函子或自然变换。此外，可以将函子态射解读为一种特殊的自然变换：恒等自然变换作用于这个函子。基于这个解读，$F \circ \alpha$便是合理的，其中$F$是从$D$到$E$的函子、$\alpha$是从$C$到$D$的自然变换，函子和自然变换当然无法复合，这个记法解读为恒等自然变换$1_F$与$\alpha$的横向复合（复合顺序先$\alpha$后$1_F$）。

Monad / 单子

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

-- Kleisli范畴中的恒等为`return :: a -> m a`、复合为`>=> :: (a -> m b) -> (b -> m c) -> (a -> m c)`
-- 尝试实现这一复合
(>=>) :: (a -> m b) -> (b -> m c) -> (a -> m c)
(>=>) f g = \a -> let mb = f a      -- 拿到一个`a`，也只能将之应用到`f`，得到`mb`
                  in mb ??? g       -- 需要`mb ??? g`，从而得到`mc`，`???`需要具备把“函子容器”打开的能力

--- ???处一般称作bind，用`>>=`表示，其定义
(>>=) :: m a -> (a -> m b) -> m b

-- 因此，一个实现了bind和return的即为一个单子m
class Monod m where
    (>>=) :: m a -> (a -> m b) -> m b
    return :: a -> m a

-- 单子m是函子，可以借助函子已有的工具来定义`>>=`
ma >>= f = ??? (fmap f ma)
-- `fmap f ma`得到了`m (m b)`类型的值，需要有个更基本的工具将“两层函子容器”解除一层，这一工具是`join`
join :: m (m a) -> m a

-- 因此，简单扩展一下函子，添加几个相当基本的函数，即可得到一个单子
class Functor m => Monad m where
    join :: m (m a) -> m a
    return :: a -> m a

以上几个概念在范畴论中的表示如下所示

在范畴论中，自函子$T$和两个自然变换$\mu$和$\eta$能够成一个单子，此外要求自然变换遵守结合律和恒等法则。

monad is a monoid in the endofunctor category.

Monad (category theory)

Monad (functional programming)

看了下维基上的相关内容，还有很多概念尚不理解，留待之后更新

What is the difference between monoid and monad?

TO BE FIXED

• Monad Update